第九讲-时间序列分析
习题8.1
1. 题目要求


2.解题过程
解:
(1)
由N=3,我们可以取预测公式: $$ M_{t+1}=\frac{y_t+y_{t-1}+y_{t-2}}{3},\ t=3,4,...,11 $$ 其中 \(M_9=133.0,M_{10}=136.8,M_{11}=137.5\) 为预测值。
预测的标准误差为: $$ S=\sqrt{\frac{\sum_{t=4}^{8}(M_t-y_t)^2}{5}}=19.3542 $$ (2)
二次指数平滑法的公式: $$ \begin{align} \begin{cases} S_t^{(1)}=\alpha y_t+(1-\alpha)S_{t-1}^{(1)}\ S_t^{(1)}=\alpha S_t^{(1)}+(1-\alpha)S_{t-1}^{(2)} \end{cases} \end{align} $$ 其中\(S_t^{(1)}\)为一次指数平滑值,\(S_t^{(2)}\)为二次指数平滑值。
当时间序列开始具有直线趋势时,建立直线指数平滑预测模型: $$ \begin{align} &\hat{y}_{t+m}=a_t+b_tm\ &\begin{cases} a_t=2S_t^{(1)}-S_t^{(2)}\ b_t=\frac{\alpha}{1-\alpha}(S_t^{(1)}-S_t^{(2)}) \end{cases} \end{align} $$ 在 \(\alpha=0.3\) 时,预测的标准误差是: $$ S=\sqrt{\frac{\sum_{t=1}^{8}(\hat{y}t-y_t)^2}{7}} = 11.7966 $$ 在 \(\alpha=0.6\) 时,预测的标准误差是: $$ S=\sqrt{\frac{\sum{t=1}^{8}(\hat{y}_t-y_t)^2}{7}} = 7.0136 $$ (3)
从上面两小问的计算过程来看,选取标准误差最小的,也即 \(\alpha=0.6\) 时的二次指数平滑模型
(4)
按照第三问的结果,取二次指数平滑模型的预测结果即可(计算过程见后文)。
\(\alpha=0.6\)时,1982年的产量预测值为152.9457亿米;1985年的产量预测为182.8640亿米
3.程序
(1)
求解的MATLAB程序如下:
clc, clear
yt = [80.8, 94.0, 88.4, 101.5, 110.3, 121.5, 134.7, 142.7];
m = length(yt);
n = 3; % 定义了移动平均窗口的大小
for i = n + 1:m + 1
% 在循环内部,用移动平均法计算 ythat 向量的当前元素值,即取窗口内最近的 n 个元素的平均值
ythat(i) = sum(yt(i-n:i-1)) / n;
end
ythat
for i = m + 1:m + n
yt(i) = ythat(i);
ythat(i+1) = sum(yt(i-n+1:i)) / n;
end
% 将 yhat 设置为 ythat 的最后四个元素
yhat = ythat(end-3:end)
% 计算原始数据 yt 和平滑后的数据 ythat 的标准差 s1
% 这里只计算从第 n+1 个元素到最后一个元素的标准差,因为前 n 个元素无法进行平滑处理
% sqrt 和 mean 分别计算标准差的平方和的平均值和标准差本身
s1 = sqrt(mean((yt(n+1:m) - ythat(n+1:m)).^2))
(2)
求解的MATLAB程序如下:(0.3和0.6都尝试一次,仅修改该数据即可)
clc, clear
yt = [80.8, 94.0, 88.4, 101.5, 110.3, 121.5, 134.7, 142.7];
n = length(yt);
% 两个平滑值
% 这里使用了简单平均法来计算 st1(1),即前三个数据点的平均值,并将其赋给 st1(1) 和 st2(1)
st1(1) = mean(yt(1:3));
st2(1) = st1(1);
% 平滑系数
alpha = 0.3;
% 循环从 i=2 开始,因为 st1(1) 和 st2(1) 已经在前面初始化了
for i = 2:n
% 使用指数平滑法更新 st1(i) 和 st2(i)
% st1(i) 的更新使用的是单次指数平滑法,而 st2(i) 的更新使用的是二次指数平滑法
st1(i) = alpha * yt(i) + (1 - alpha) * st1(i-1);
st2(i) = alpha * st1(i) + (1 - alpha) * st2(i-1);
end
% 计算趋势系数 at 和 bt
at = 2 * st1 - st2;
bt = alpha / (1 - alpha) * (st1 - st2);
% 计算预测值 yhat
yhat = at + bt;
sigma = sqrt(mean((yt(2:end) - yhat(1:end-1)).^2));
% 根据模型预测最后一个数据点后的趋势,进一步预测接下来四个数据点的值
m = 1:4;
yhat2 = at(end) + bt(end) * m;
sigma
yhat2
4.结果
(1)

(2)
在 \(\alpha=0.3\) 时

在 \(\alpha=0.6\) 时

(3)
选取标准误差最小的,也即 \(\alpha=0.6\) 时的二次指数平滑模型
(4)
最终结果:1982年的产量预测值为152.9457亿米;1985年的产量预测为182.8640亿米
习题8.2
1. 题目要求
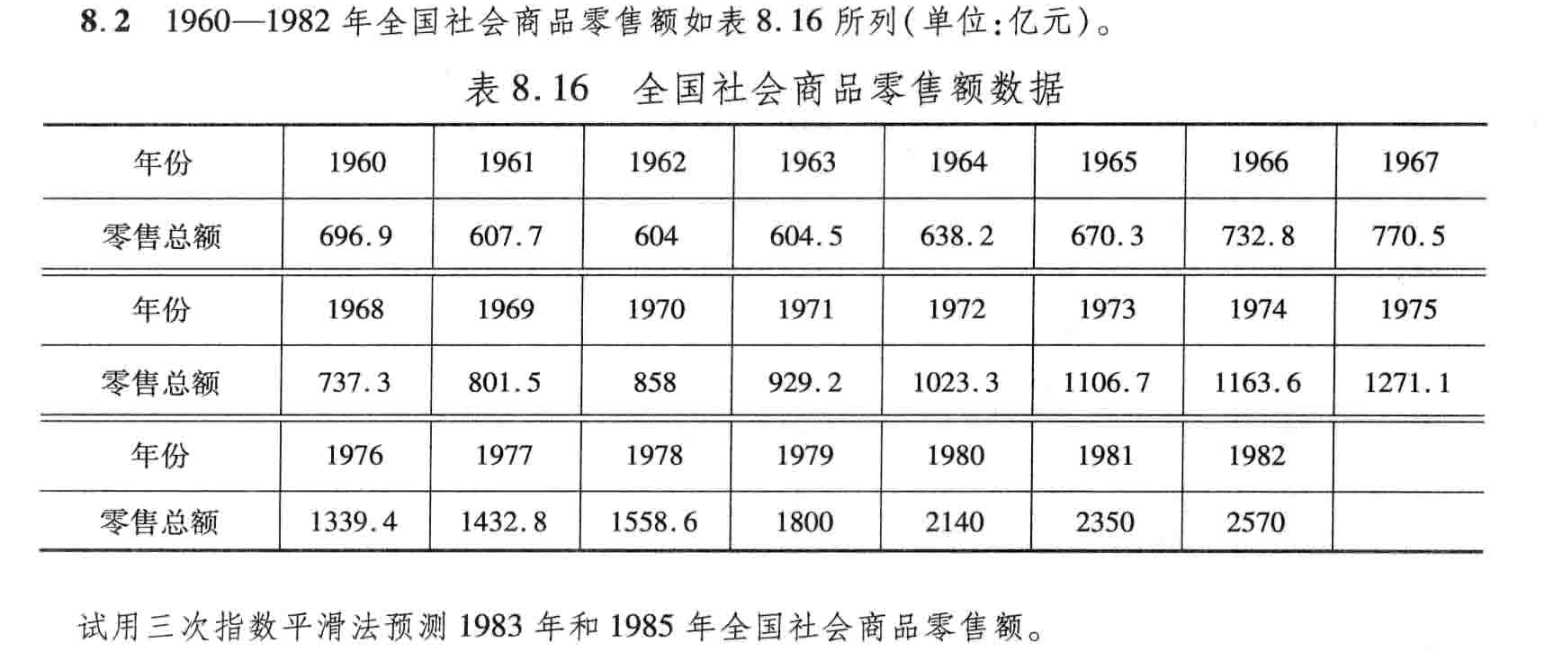
2.解题过程
解:
计算公式为: $$ \begin{align} \begin{cases} S_t^{(1)}=\alpha y_t+(1-\alpha)S_{t-1}^{(1)}\ S_t^{(2)}=\alpha S_t^{(1)}+(1-\alpha)S_{t-1}^{(2)}\ S_t^{(3)}=\alpha S_t^{(2)}+(1-\alpha)S_{t-1}^{(3)} \end{cases} \end{align} $$ 其中 \(S_t^{(1)},S_t^{(2)},S_t^{(3)}\) 分别是一、二、三次指数平滑值。
初始值计算如下: $$ S_0^{(1)}=S_0^{(2)}=S_0^{(3)}=\frac{y_1+y_2+y_3}{3}=636.2 $$ 预测模型为: $$ \hat{y}_{t+m}=a_t+b_tm+c_tm^2,m=1,2,... $$
t=23时,计算结果如下: $$ a_{23}=2572.2613,b_{23}=259.3374,c_{23}=8.9819 $$
最终求得:1983、1985年的预测值分别为 2840.58058505076 亿元,3431.11062220508 亿元
3.程序
求解的MATLAB程序如下:
clc, clear
% yt记录零售总额数据
yt = [696.9, 607.7, 604, 604.5, 638.2, 670.3, 732.8, 770.5, ...
737.3, 801.5, 858, 929.2, 1023.3, 1106.7, 1163.6, 1271.1, ...
1339.4, 1432.8, 1558.6, 1800, 2140, 2350, 2570]';
n = length(yt);
alpha = 0.3; % 意味着对于当前时刻的预测,历史数据的权重为 0.7,预测数据的权重为 0.3
st0 = mean(yt(1:3)); % 计算数据向量中前三个数据的平均值,并将其设置为初始平滑值st0
% 计算三次指数平滑法中的一阶平滑值st1、二阶平滑值st2和三阶平滑值st3的初始值
st1(1) = alpha * yt(1) + (1 - alpha) * st0;
st2(1) = alpha * st1(1) + (1 - alpha) * st0;
st3(1) = alpha * st2(1) + (1 - alpha) * st0;
% 使用循环计算每个时刻的一阶平滑值st1、二阶平滑值st2和三阶平滑值st3
for i = 2:n
st1(i) = alpha * yt(i) + (1 - alpha) * st1(i-1);
st2(i) = alpha * st1(i) + (1 - alpha) * st2(i-1);
st3(i) = alpha * st2(i) + (1 - alpha) * st3(i-1);
end
% 根据三次指数平滑法的公式,计算出平滑后的数据yhat、趋势项系数bt和季节项系数ct
at = 3 * st1 - 3 * st2 + st3;
bt = 0.5 * alpha / (1 - alpha)^2 * ...
((6 - 5 * alpha) * st1 - 2 * (5 - 4 * alpha) * st2 + (4 - 3 * alpha) * st3);
ct = 0.5 * alpha^2 / (1 - alpha)^2 * ...
(st1 - 2 * st2 + st3);
yhat = at + bt + ct;
xishu = [ct(end), bt(end), at(end)]
yuce = polyval(xishu, [1:3]) % 计算未来三年的预测值
4.结果
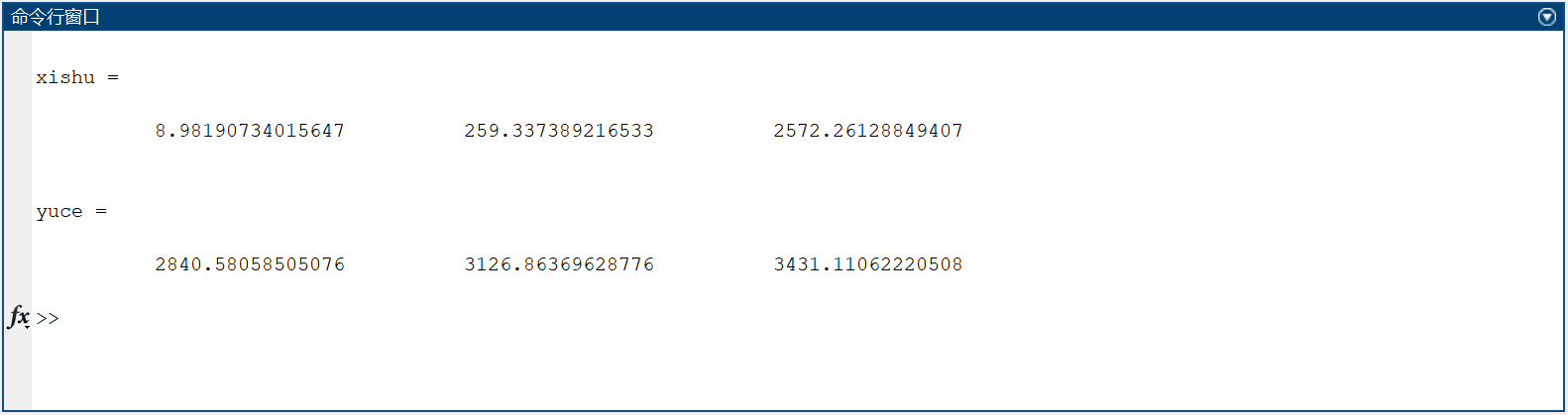
1983、1985年的预测值分别为 2840.58058505076 亿元,3431.11062220508 亿元
习题8.3
1. 题目要求

2.解题过程
解:
本题我选取了两个曲线。
(1)Compertz曲线
一般形式为: $$ \hat{y}t=Ka^{b^t},K>0,0<a\neq1,0<b\neq1 $$ 两边取对数 $$ \ln\hat{y}_t=\ln K+b^t\ln a $$ 记 $$ \hat{y}'_t = \ln\hat{y},K'=\ln K,a'=\ln a $$ 则 $$ \hat{y}'_t=K'+a'b^t $$ 三和法估计参数: $$ S_1=\sum{t=1}^{m}y't,S_1=\sum{t=m+1}^{2m}y't,S_1=\sum{t=2m+1}^{3m}y'_t $$ 则 $$ \begin{align} \begin{cases} b&=(\frac{S_3-S_2}{S_2-S_1})^{\frac{1}{m}}\ a'&=(S_2-S_1)\frac{b-1}{b(b^m-1)^2}\ K'&=\frac{1}{m}[S_1-\frac{a'b(b^m-1)}{b-1}] \end{cases} \end{align} $$ 解得 $$ b=0.8244,a'=-1.7075,a=0.1813,K'=2.5804,K=13.2021 $$ 所以Comperz曲线方程为: $$ \hat{y}_t=13.2021\times 0.1813^{0.8244^t} $$ 1985年,1990年的粮食产量分别为12.3830,12.8840
(2)Logistic曲线
一般形式为: $$ \frac{d y}{d x}=ry(1-\frac{y}{L}) $$ 解此微分方程: $$ y=\frac{L}{1+ce^{-rt}} $$ 记Logistic曲线一般形式为: $$ y_t=\frac{1}{K+ab^t},K>0,a>0,0<b\neq1 $$ 令 \(y'_t=\frac{1}{y_t}\) 得: $$ y't=K+ab^t $$ 三和法估计参数: $$ S_1=\sum{t=1}^{m}y't,S_1=\sum{t=m+1}^{2m}y't,S_1=\sum{t=2m+1}^{3m}y'_t $$ 则 $$ \begin{align} \begin{cases} b=(\frac{S_3-S_2}{S_2-S_1})^{\frac{1}{m}}\ a=(S_2-S_1)\frac{b-1}{b(b^m-1)^2}\ K=\frac{1}{m}[S_1-\frac{a'b(b^m-1)}{b-1}] \end{cases} \end{align} $$ 解得 $$ b=0.7501,a=0.2796,K=0.0805 $$ 所以Logistic曲线方程为: $$ \hat{y}_t=\frac{1}{0.0805+0.2796\times0.7501^t} $$ 1985年,1990年的粮食产量分别为12.1068,12.3467
3.程序
(1)
求解的MATLAB程序如下:
clc, clear
y = [3.78, 4.19, 4.83, 5.46, 6.71, 7.99, 8.60, 9.24, ...
9.67, 9.87, 10.49, 10.92, 10.93, 12.39, 12.59];
yt = log(y); % 将y取自然对数,以便进行Compertz曲线拟合
n = length(yt);
m = n / 3;
% 计算yt的长度n和m,m是将时间分成三段后的长度
% Compertz曲线需要将时间分成三个等长的部分
% 计算yt的前1/3、中间1/3和后1/3的和
s1 = sum(yt(1:m));
s2 = sum(yt(m+1:2*m));
s3 = sum(yt(2*m+1:3*m));
b = ((s3 - s2) / (s2 - s1))^(1 / m); % b控制曲线的形状
a = (s2 - s1) * (b - 1) / (b * (b^m - 1)^2); % a控制曲线的位置
k = (s1 - a * b * (b^m - 1) / (b - 1)) / m; % k是拟合曲线的最小值
a = exp(a);
k = exp(k); % 对a和k值进行指数运算,以将其还原为实际值
yuce = @(t) k * a.^(b.^t); % 创建一个匿名函数
ypre = yuce([n + 2, n + 7])
(2)
求解的MATLAB程序如下:
clc, clear
y = [3.78, 4.19, 4.83, 5.46, 6.71, 7.99, 8.60, 9.24, ...
9.67, 9.87, 10.49, 10.92, 10.93, 12.39, 12.59];
yt = 1 ./ y;
% yt向量的长度n和分成三组时每组的长度m
n = length(yt);
m = n / 3;
% 每组的元素之和
s1 = sum(yt(1:m));
s2 = sum(yt(m+1:2*m));
s3 = sum(yt(2*m+1:3*m));
% 使用Logistic曲线拟合yt向量。变量b是增长率,变量a是曲线的形状,变量k是曲线的位置
b = ((s3 - s2) / (s2 - s1))^(1 / m);
a = (s2 - s1) * (b - 1) / (b * (b^m - 1)^2);
k = (s1 - a * b * (b^m - 1) / (b - 1)) / m;
yuce = @(t) 1 ./ (k + a * b.^t);
ypre = yuce([n + 2, n + 7])
4.结果
