第八讲-回归分析

习题11.1

1. 题目要求

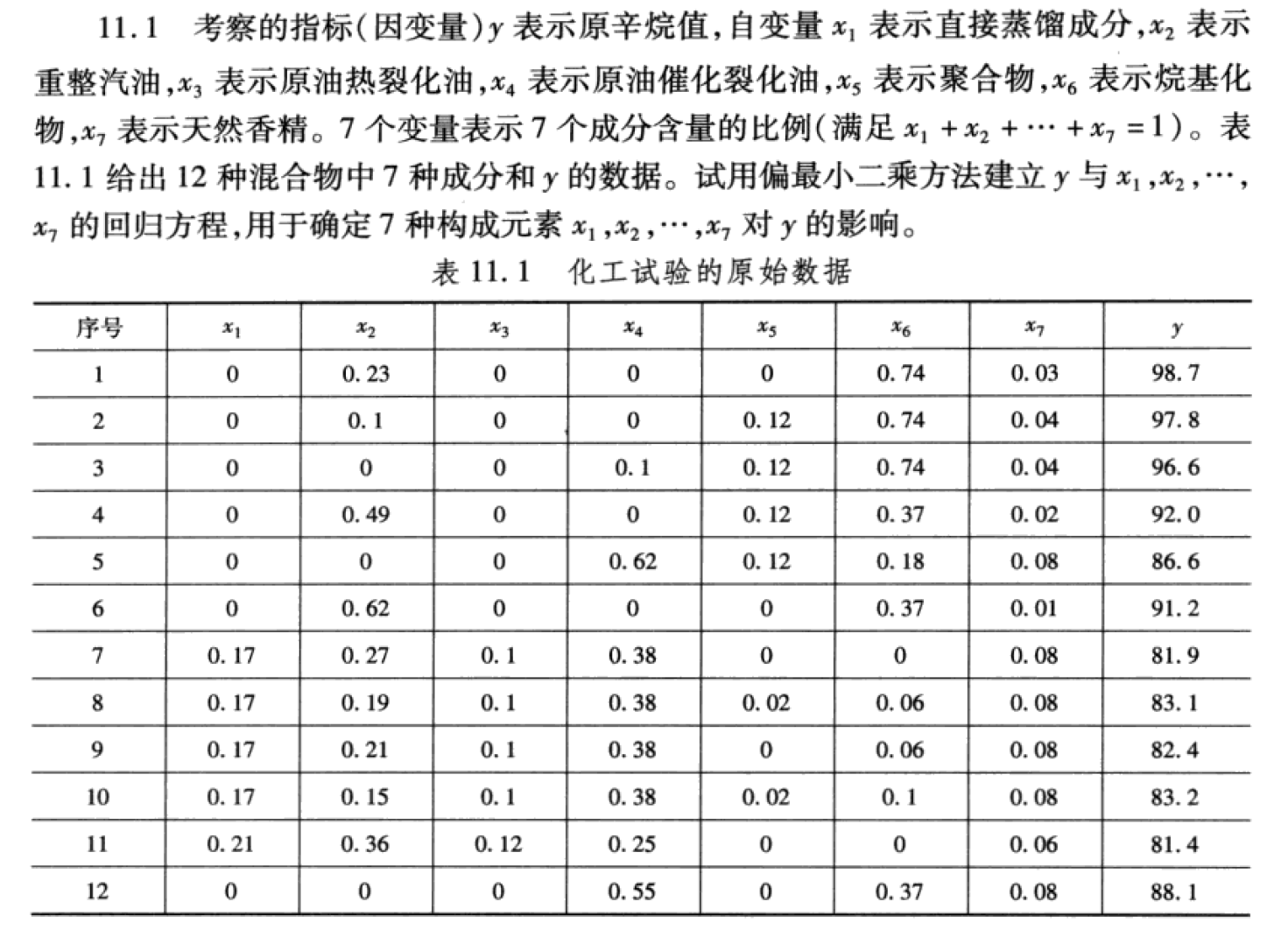
2.解题过程

解：

12个样本点分别用 i=1,...,12 表示各个样本点，自变量的观测数据矩阵即为$A=(a_{ij})_{12\times7}$，因变量的观测数据矩阵即为$B = [b_1,...,b_{12}]^T$。

（1）

数据标准化

将各指标值$a_{ij}$转换成标准化指标值$\tilde{a_{ij}}$，即 $$ \tilde{a_{ij}} = \frac{a_{ij}-\mu_j^{(1)}}{s_{j}^{(1)}},\qquad i=1,2,...,12,j=1,...,7. $$ 式中： $$ \mu_j^{(1)}=\frac{1}{12}\sum_{i=1}^{12}a_{ij}, \ s_j^{(1)} = \sqrt{\frac{1}{12-1}\sum_{i=1}^{12}(a_{ij}-\mu_{j}^{(1)})^2},(j=1,...,7) , $$ 即$\mu_{j}^{(1)}$、$s_{j}^{(1)}$为第j个自变量$x_j$的样本均值和样本标准差。对应地，称 $$ \tilde{x_j}=\frac{x_j - \mu_{j}^{(1)}}{s_{j}^{(1)}},j=1,...,7. $$ 为标准化指标变量。

类似地，将$b_i$转换成标准化指标值$\tilde{b_i}$，即 $$ b_i = \frac{b_i-\mu^{(2)}}{s^{(2)}},i=1,2,...,12, $$ 式中： $$ \mu^{(2)}=\frac{1}{12}\sum_{i=1}^{12}b_i\ s^{(2)}=\sqrt{\frac{1}{12-1}\sum_{i=1}^{12}(b_{i}-\mu^{(2)})^2} $$ 即$\mu^{(2)},s^{(2)}$为因变量y的样本均值和样本标准差；

对应地，称 $$ \tilde{y} = \frac{y-\mu^{(2)}}{s^{(2)}} $$ 为对应的标准化变量。

（2）

分别提出自变量组和因变量组的成分。使用matlab求得7对成分，其中第一对成分为 $$ \begin{equation} \begin{cases} \mu_1&=-0.0906\tilde{x_1}-0.0575\tilde{x}_2-0.0804\tilde{x}_3-0.116\tilde{x}_4+0.0238\tilde{x}_5-0.0657\tilde{x}_7,\ v_1&=3.1874\tilde{y}_1.
\end{cases} \end{equation} $$ 前三个成分解释自变量的比率为91.83%，只要取3对成分即可。

（3）

求三个成分对标准化指标变量与成分变量之间的回归方程，求得自变量组和因变量组与$u_1、u_2、u_3$之间的回归方程分别为：

$$ \tilde{x}_1 = -2.9991u_1-0.1186u_2+1.0472u_3, $$

$$ \tilde{x}_2 = 0.2095u_1-2.7981u_2+1.7237u_3, $$

......

$$ \tilde{x}_7 = -2.7279u_1+1.3298u_2-1.3002u_3, $$

$$ \tilde{y}_1 = 3.1874u_1+0.7617u_2+0.3954u_3, $$

（4）

求因变量组与自变量组之间的回归方程

把（2）中成分$u_i$代入（3）中的回归方程，得到标准化指标变量的回归方程为： $$ \tilde{y}_1 = -0.1391\tilde{x}_1-0.2087\tilde{x}_2-0.1376\tilde{x}_3-0.2932\tilde{x}_4

-0.0384\tilde{x}_5+0.4564\tilde{x}_6-0.1434\tilde{x}_7. $$ 将标准化变量$\tilde{y},\tilde{x}_j,(j=1,...,7)$分别还原成原始变量$y,x_j$，就可以得到结果。

3.程序

求解的MATLAB程序如下：

clc, clear

% 导入数据
ab0 = [0, 0.23, 0, 0, 0, 0.74, 0.03, 98.7; ...
    0, 0.1, 0, 0, 0.12, 0.74, 0.04, 97.8; ...
    0, 0, 0, 0.1, 0.12, 0.74, 0.04, 96.6; ...
    0, 0.49, 0, 0, 0.12, 0.37, 0.02, 92.0; ...
    0, 0, 0, 0.62, 0.12, 0.18, 0.08, 86.6; ...
    0, 0.62, 0, 0, 0, 0.37, 0.01, 91.2; ...
    0.17, 0.27, 0.1, 0.38, 0, 0, 0.08, 81.9; ...
    0.17, 0.19, 0.1, 0.38, 0.02, 0.06, 0.08, 83.1; ...
    0.17, 0.21, 0.1, 0.38, 0, 0.06, 0.08, 82.4; ...
    0.17, 0.15, 0.1, 0.38, 0.02, 0.1, 0.08, 83.2; ...
    0.21, 0.36, 0.12, 0.25, 0, 0, 0.06, 81.4; ...
    0, 0, 0, 0.55, 0, 0.37, 0.08, 88.1];
% 均值和方差
mu = mean(ab0);
sig = std(ab0);
% 标准化以后的自变量和因变量数据
ab = zscore(ab0);
a = ab(:, [1 : 7]);
b = ab(:, [8: end]);

% 主成分的个数3
[XL, YL, XS, YS, BETA, PCTVAR, MSE, stats] = plsregress(a, b, 3);

n = size(a, 2);
m = size(b, 2);

format long g
BETA2(1, :) = mu(n + 1 : end) - mu(1:n) ./ sig(1:n) * BETA([2 : end], :) .* sig(n + 1 :end);
BETA2([2: n + 1], :) = (1 ./ sig(1:n))' * sig(n + 1 : end) .* BETA([2: end], :)

%直方图
bar(BETA','k');

4.结果

所以，最终建立的回归方程如下： $$ \begin{aligned} y &= 92.6759894798203 -9.82831779652421 \times x_1 -6.96018146108128 \times x_2 -16.6662390524996 \times x_3 \ &\quad -8.4218024072797\times x_4 -4.38893380525098 \times x_5 +10.1613044805558\times x_6 \ &\quad-34.5289588223774 \times x_7 \ \end{aligned} $$

习题7.2

1. 题目要求

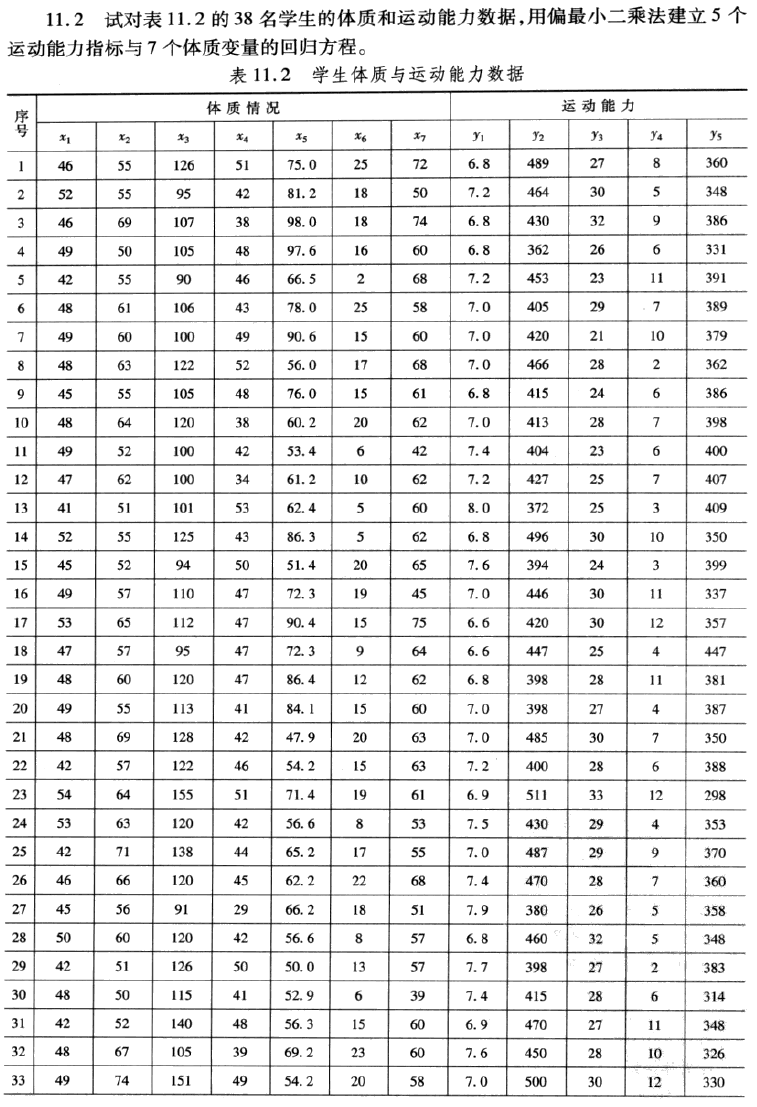
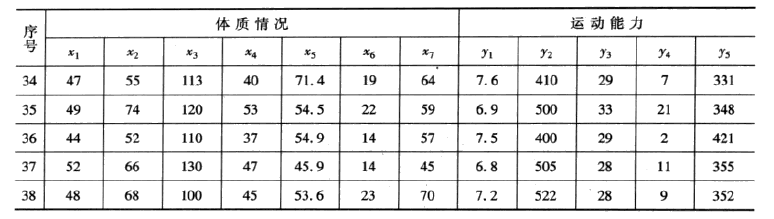
2.解题过程

解：

解题思路与方法与上一题类似，本题不再详细赘述。

不同点在于，本题一共有5对成分。

3.程序

求解的MATLAB程序如下：

clc, clear

% 导入数据
ab0 = [46, 55, 126, 51, 75.0, 25, 72, 6.8, 489, 27, 8, 360; ...
    52, 55, 95, 42, 81.2, 18, 50, 7.2, 464, 30, 5, 348; ...
    46, 69, 107, 38, 98.0, 18, 74, 6.8, 430, 32, 9, 386; ...
    49, 50, 105, 48, 97.6, 16, 60, 6.8, 362, 26, 6, 331; ...
    42, 55, 90, 46, 66.5, 2, 68, 7.2, 453, 23, 11, 391; ...
    48, 61, 106, 43, 78.0, 25, 58, 7.0, 405, 29, 7, 389; ...
    49, 60, 100, 49, 90.6, 15, 60, 7.0, 420, 21, 10, 379; ...
    48, 63, 122, 52, 56.0, 17, 68, 7.0, 466, 28, 2, 362; ...
    45, 55, 105, 48, 76.0, 15, 61, 6.8, 415, 24, 6, 386; ...
    48, 64, 120, 38, 60.2, 20, 62, 7.0, 413, 28, 7, 398; ...
    49, 52, 100, 42, 53.4, 6, 42, 7.4, 404, 23, 6, 400; ...
    47, 62, 100, 34, 61.2, 10, 62, 7.2, 427, 25, 7, 407; ...
    41, 51, 101, 53, 62.4, 5, 60, 8.0, 372, 25, 3, 409; ...
    52, 55, 125, 43, 86.3, 5, 62, 6.8, 496, 30, 10, 350; ...
    45, 52, 94, 50, 51.4, 20, 65, 7.6, 394, 24, 3, 399; ...
    49, 57, 110, 47, 72.3, 19, 45, 7.0, 446, 30, 11, 337; ...
    53, 65, 112, 47, 90.4, 15, 75, 6.6, 420, 30, 12, 357; ...
    47, 57, 95, 47, 72.3, 9, 64, 6.6, 447, 25, 4, 447; ...
    48, 60, 120, 47, 86.4, 12, 62, 6.8, 398, 28, 11, 381; ...
    49, 55, 113, 41, 84.1, 15, 60, 7.0, 398, 27, 4, 387; ...
    48, 69, 128, 42, 47.9, 20, 63, 7.0, 485, 30, 7, 350; ...
    42, 57, 122, 46, 54.2, 15, 63, 7.2, 400, 28, 6, 388; ...
    54, 64, 155, 51, 71.4, 19, 61, 6.9, 511, 33, 12, 298; ...
    53, 63, 120, 42, 56.6, 8, 53, 7.5, 430, 29, 4, 353; ...
    42, 71, 138, 44, 65.2, 17, 55, 7.0, 487, 29, 9, 370; ...
    46, 66, 120, 45, 62.2, 22, 68, 7.4, 470, 28, 7, 360; ...
    45, 56, 91, 29, 66.2, 18, 51, 7.9, 380, 26, 5, 358; ...
    50, 60, 120, 42, 56.6, 8, 57, 6.8, 460, 32, 5, 348; ...
    42, 51, 126, 50, 50.0, 13, 57, 7.7, 398, 27, 2, 383; ...
    48, 50, 115, 41, 52.9, 6, 39, 7.4, 415, 28, 6, 314; ...
    42, 52, 140, 48, 56.3, 15, 60, 6.9, 470, 27, 11, 348; ...
    48, 67, 105, 39, 69.2, 23, 60, 7.6, 450, 28, 10, 326; ...
    49, 74, 151, 49, 54.2, 20, 58, 7.0, 500, 30, 12, 330; ...
    47, 55, 113, 40, 71.4, 19, 64, 7.6, 410, 29, 7, 331; ...
    49, 74, 120, 53, 54.5, 22, 59, 6.9, 500, 33, 21, 348; ...
    44, 52, 110, 37, 54.9, 14, 57, 7.5, 400, 29, 2, 421; ...
    52, 66, 130, 47, 45.9, 14, 45, 6.8, 505, 28, 11, 355; ...
    48, 68, 100, 45, 53.6, 23, 70, 7.2, 522, 28, 9, 352];

% 均值和方差
mu = mean(ab0);
sig = std(ab0);
% 标准化以后的自变量和因变量数据
ab = zscore(ab0);
a = ab(:, [1 : 7]);
b = ab(:, [8: end]);

% 主成分个数5
[XL, YL, XS, YS, BETA, PCTVAR, MSE, stats] = plsregress(a, b, 5);

n = size(a, 2);
m = size(b, 2);

format long g
BETA2(1, :) = mu(n + 1 : end) - mu(1:n) ./ sig(1:n) * BETA([2 : end], :) .* sig(n + 1 :end);
BETA2([2: n + 1], :) = (1 ./ sig(1:n))' * sig(n + 1 : end) .* BETA([2: end], :)

%直方图
bar(BETA', 'k');

4.结果

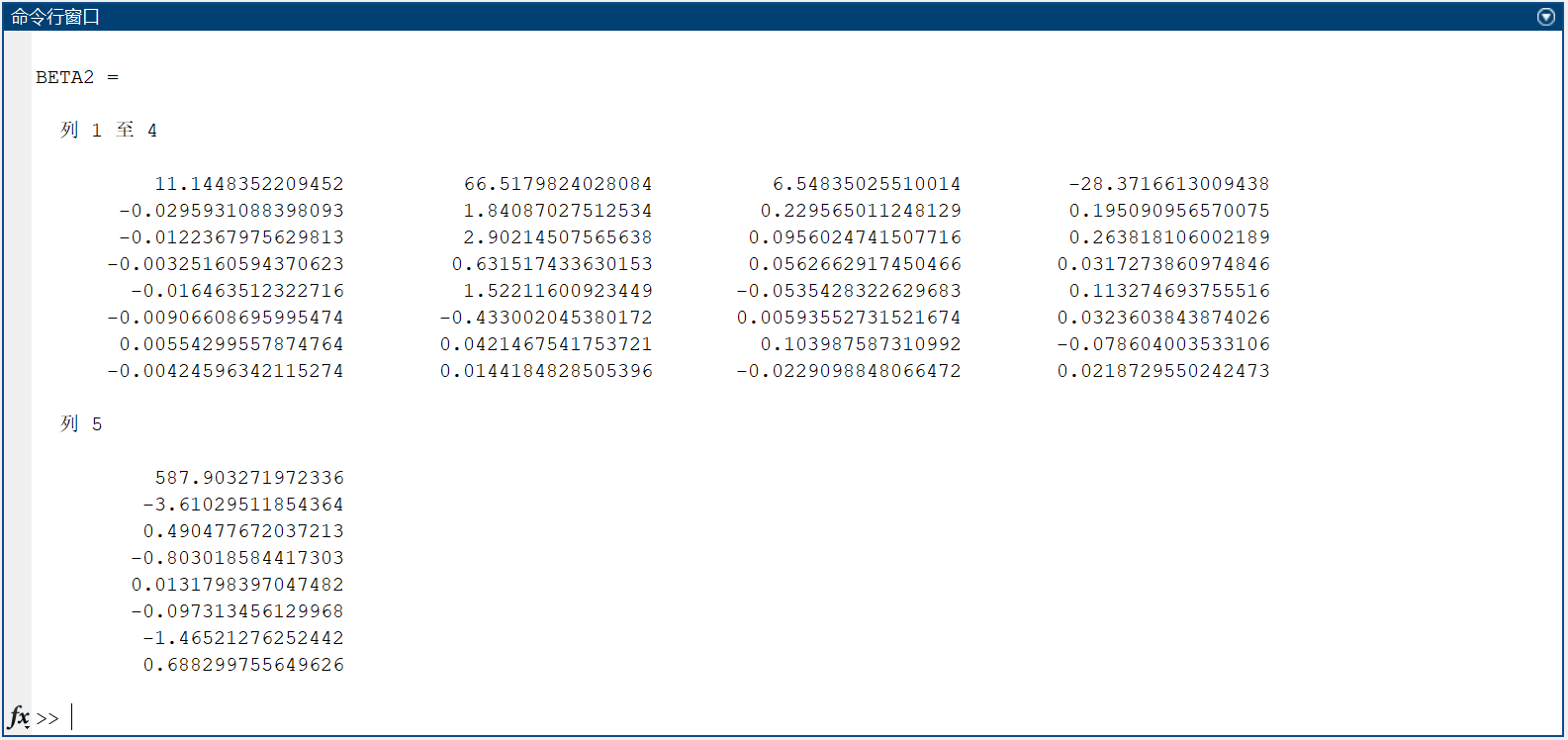
所以，最终建立的回归方程如下： $$ \begin{aligned} y_1 &= 11.1448352209452 - 0.0295931088398093 \times x_1 - 0.0122367975629813 \times x_2 - 0.00325160594370623 \times x_3 \ &\quad - 0.016463512322716 \times x_4 - 0.00906608695995474 \times x_5 + 0.00554299557874764 \times x_6 \ &\quad- 0.00424596342115274 \times x_7 \ y_2 &= 66.5179824028084 + 1.84087027512534 \times x_1 + 2.90214507565638 \times x_2 + 0.631517433630153 \times x_3 \ &\quad + 1.52211600923449 \times x_4 - 0.433002045380172 \times x_5 + 0.0421467541753721 \times x_6 \ &\quad+ 0.0144184828505396 \times x_7 \ y_3 &= 6.54835025510014 + 0.229565011248129 \times x_1 + 0.0956024741507716 \times x_2 + 0.0562662917450466 \times x_3 \ &\quad - 0.0535428322629683 \times x_4 + 0.00593552731521674 \times x_5 + 0.103987587310992 \times x_6 \ &\quad- 0.0229098848066472 \times x_7 \ y_4 &= -28.3716613009438 + 0.195090956570075 \times x_1 + 0.263818106002189 \times x_2 + 0.0317273860974846 \times x_3 \ &\quad + 0.113274693755516 \times x_4 + 0.0323603843874026 \times x_5 - 0.078604003533106 \times x_6 \ &\quad+ 0.0218729550242473 \times x_7 \ y_5 &= 587.903271972336 - 3.61029511854364 \times x_1 + 0.490477672037213 \times x_2 - 0.803018584417303 \times x_3 \ &\quad + 0.0131798397047482 \times x_4 - 0.097313456129968 \times x_5 - 1.46521276252442 \times x_6 \ &\quad+ 0.688299755649626 \times x_7 \ \end{aligned} $$