第七讲-Bootstrap方法

习题7.3

1. 题目要求

2.解题过程

解：

相继地、独立地自原始样本数据用放回抽样的方法，得到10000个容量均为5的Bootstrap 样本。

对每个Bootstrap样本算出样本均值 $\overline{{{x}}}_{i}^{\,^{\ast}}(i=1,2,\cdots,10000)$ ，将10000个 ${\overline{{x}}}^{*}$ 按自小到大排序，左起第500位为 ${\overline{{x}}}_{(500)}^{*}=1098$ ，左起第9500位为 ${\overline{{x}}}_{(9500)}^{*}=1232$ ，于是得 μ 的一个置信水平为0.90的Bootstrap置信区间为 $$ ({\overline{{x}}}_{(500)}^{},{\overline{{x}}}_{(9500)}^{})=(1098,1232) $$

3.程序

求解的MATLAB程序如下：

clc, clear

a = [1050, 1100, 1120, 1250, 1280];
b = bootci(10000, {@ (x)mean(x), a}, 'alpha', 0.1);
b

4.结果

得 μ 的一个置信水平为0.90的Bootstrap置信区间为: $$ ({\overline{{x}}}_{(500)}^{},{\overline{{x}}}_{(9500)}^{})=(1098,1232) $$

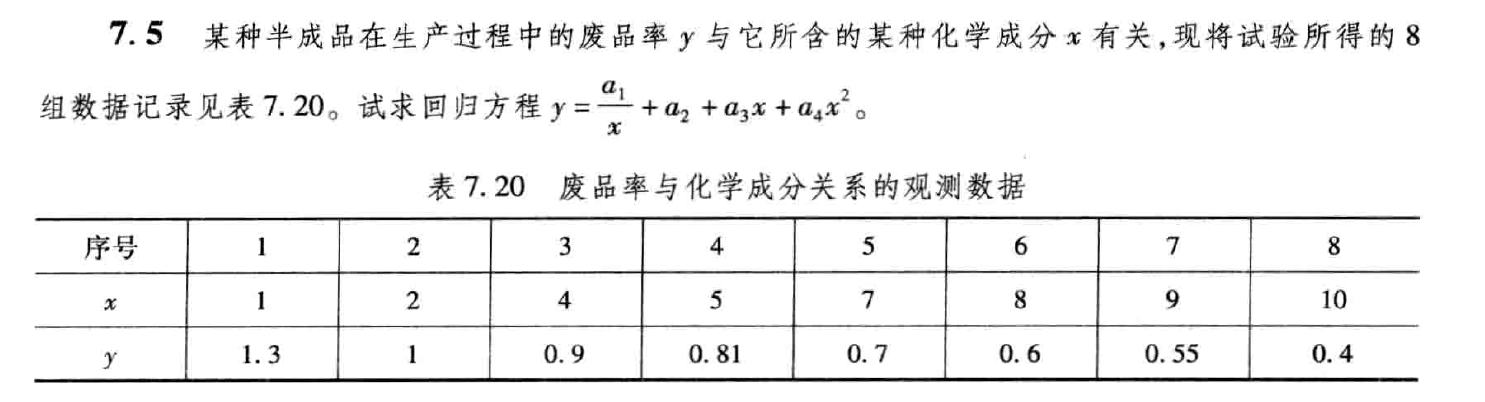
习题7.5

1. 题目要求

2.解题过程

解：

求解 x 和 y 之间的回归方程，即一个能够最佳拟合这些数据的线性模型.

构造线性方程组的系数矩阵 b。它由四列组成，分别是 1/x、1、x 和 x 的平方。这些列的选择基于假设的线性关系形式，但也可以根据具体的问题进行调整。需要注意的是，已经对 x 取了转置，使其成为一个列向量。

求出的系数矩阵如下： $$ b= \begin{bmatrix} 1.0000 & 1.0000 & 1.0000 & 1.0000 \ 0.5000 & 1.0000 & 2.0000 & 4.0000 \ 0.2500 & 1.0000 & 4.0000 & 16.0000 \ 0.2000 & 1.0000 & 5.0000 & 25.0000 \ 0.1429 & 1.0000 & 7.0000 & 49.0000 \ 0.1250 & 1.0000 & 8.0000 & 64.0000 \ 0.1111 & 1.0000 & 9.0000 & 81.0000 \ 0.1000 & 1.0000 & 10.0000 & 100.0000 \ \end{bmatrix} $$ 最后，使用反斜杠符号求解线性方程组的最小二乘解。具体来说，它使用了正规方程的方法，即求解 $(b^T b)^{-1} b^T y$，其中 $b^T$ 表示 b 的转置，$^{-1}$ 表示矩阵的逆，$y$ 表示因变量的向量。最终的结果是一个包含了四个系数的列向量，分别对应于 b 矩阵的四列。这些系数定义了回归方程的形式，可以用于预测新的因变量值。

最终求解得到的回归方程为： $$ y={\frac{0.6498}{x}}+0.5901+0.0666x-0.0091x^{2}, $$

3.程序

求解的MATLAB程序如下：

clc, clear

x = [1, 2, 4, 5, 7, 8, 9, 10]';
y = [1.3, 1, 0.9, 0.81, 0.7, 0.6, 0.55, 0.4]';

b = [1 ./ x, ones(size(x)), x, x.^2] % 构造线性方程组的系数矩阵
% 这一行代码构造了线性方程组的系数矩阵 b。它由四列组成，分别是 1/x、1、x 和 x 的平方

% 使用反斜杠符号求解线性方程组的最小二乘解
cs = b \ y % 求最小二乘解

4.结果

回归方程为： $$ y={\frac{0.6498}{x}}+0.5901+0.0666x-0.0091x^{2}, $$