跳转至

第六讲-假设检验

习题7.1

1. 题目要求

image-20230410210522550

2.解题过程

解：

（1）

首先，数学方法分析。

平均值和方差都未知的时候，灯泡寿命平均值 $ \mu $ 的置信度为0.90的置信区间为： $$ \left(\overline{{X}}\,-\,\frac{S}{\sqrt{n}}t_{\alpha/2}\left(\,n\,-\,1\,\right)\,,\overline{{X}}\,+\,\frac{S}{\sqrt{n}}t_{\alpha/2}\left(\,n\,-\,1\,\right)\,\right) $$ 这里，其中： $$ 1\,-\,\alpha=0.9\,,\alpha=0.1\,,\alpha/2=0.05\,,n=5\,,n\,-1=4 $$ 通过计算可以得到： $$ \stackrel{-}{x}~=\;\frac{1}{5}\sum_{i=1}^{5}{x_{i}}~=~1160 \ s^{2}\;=\;\frac{1}{4}\sum_{i=1}^{4}\;\;(\;x_{i}\,-\,\overline{{{x}}}\,)^{2}\;=\;99.7484 $$ 接下来，通过代入公式，就可以求出置信区间（答案见后）。

（2）

其次，本题有着MATLAB专门的函数可以较为简便地求出结果。

在MATLAB中，ttest函数是进行单样本或双样本t检验的函数。t检验是一种常见的假设检验方法，用于比较两个样本的均值是否相等，或者一个样本的均值是否等于一个已知的值。

ttest函数的语法如下：

[h,p,ci,stats] = ttest(data,mu)
[h,p,ci,stats] = ttest(data1,data2)

其中，第一种情况是单样本t检验，第二种情况是双样本t检验。具体参数说明如下：

  • data：需要进行t检验的数据样本，可以是一个向量或矩阵。
  • mu：单样本t检验中的假设均值。
  • data1、data2：双样本t检验中的两组数据样本，可以是向量或矩阵，但必须大小相同。
  • h：表示是否拒绝原假设的逻辑值，1表示拒绝原假设，0表示不拒绝原假设。
  • p：表示计算得到的p值，即原假设成立的概率。
  • ci：表示置信区间，即均值的真实值有95%的可能在这个区间内。
  • stats：包含检验统计量和自由度的结构体。

需要注意的是，ttest函数默认使用双侧检验，也就是假设均值不等于指定的值。如果需要使用单侧检验，可以通过设置alpha参数来实现。

本题，直接使用ttest函数即可解决。

3.程序

求解的MATLAB程序如下：

clc, clear

% 数据
age = [1050, 1100, 1120, 1250, 1280];

% 按照格式调用ttest函数
[h, p, ci, stats] = ttest(age, mean(age), 'Alpha', 0.1);

% ci就是置信区间
format long g
ci

4.结果

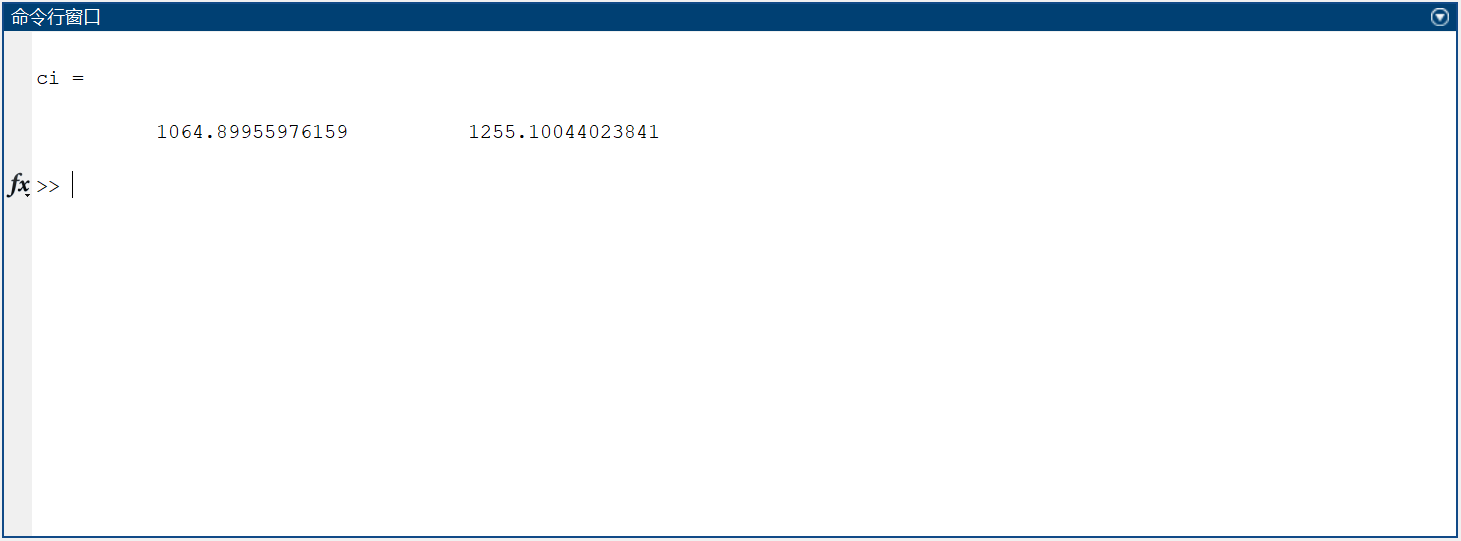
image-20230410203928922

求出的总体均值的置信水平为0.90的置信区间为：（1064.90 , 1255.10）

习题7.2

1. 题目要求

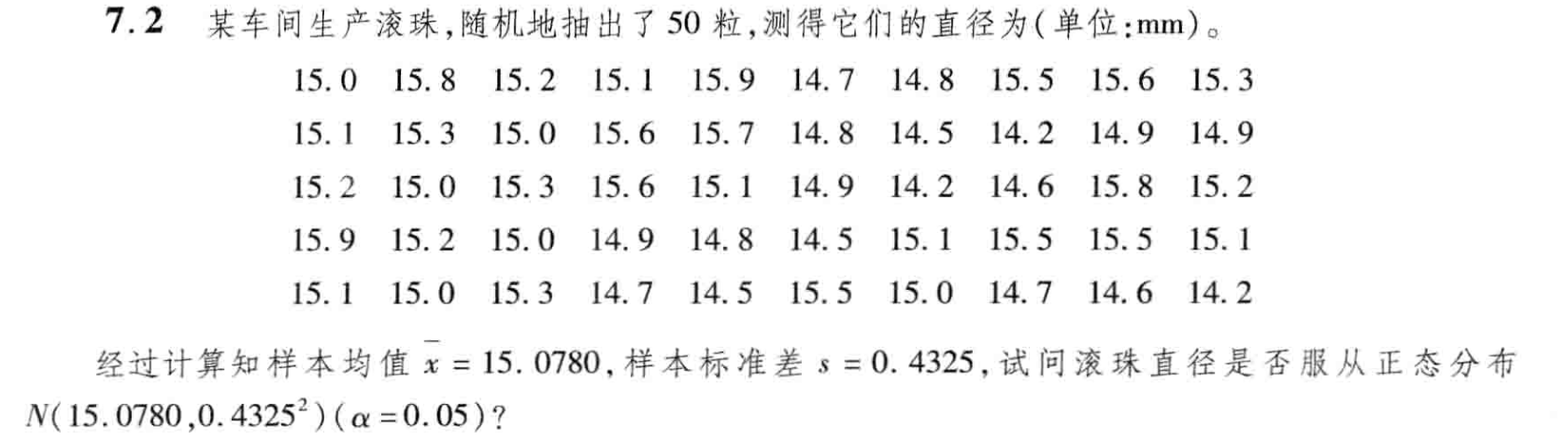
image-20230410210846533

2.解题过程

解：

这一题，我决定采用柯尔莫哥洛夫(Kolmogorov-Smirnov) 检验的方法来做。

（1）

下面是数学方法分析：

假设 $$ H_0: X服从N(\mu,\sigma^{2}) \ H_1: X不服从N(\mu,\sigma^{2}) $$ 由于题目中直接给出了均值和标准差，所以直接代入。

拒绝域为（其中n=50）： $$ D_{n}\geq{\frac{1.36}{\sqrt{n}}} $$ 计算： $$ D_n=\operatorname*{sup}{x{i}}\mid F_{n}(\,x_{i})\;-F(\,x_{i}\,)\;\mid $$

如果最终计算结果不在拒绝域，则认为原假设成立。

（2）

其次，本题有着MATLAB专门的函数可以较为简便地求出结果。

KS检验(Kolmogorov-Smirnov Test)是一种非参数的假设检验方法，它用于检验一个样本是否符合特定的概率分布或者两个样本是否来自于同一分布。该方法可以用于连续或离散分布。

[h, p, ksstat] = kstest(x, y)

其中，x和y是要进行KS检验的两个样本数据（必须是向量），h是假设检验的结果，p是对应的P值，ksstat是KS统计量。

当h为1时，说明拒绝原假设，即两个样本不来自同一个分布或单个样本不来自指定分布；

当h为0时，说明不能拒绝原假设，即两个样本来自同一个分布或单个样本来自指定分布。

p值越小，说明越不可能两个样本来自同一个分布或单个样本来自指定分布。常用的显著性水平是0.05和0.01。如果p值小于显著性水平，就拒绝原假设。

ksstat是KS统计量，表示两个样本的最大差异。它的值越大，说明两个样本越不可能来自同一个分布或单个样本越不可能来自指定分布。

3.程序

求解的MATLAB程序如下：

clc, clear

diameters = [15.0, 15.8, 15.2, 15.1, 15.9, 14.7, 14.8, 15.5, 15.6, 15.3, ...
    15.1, 15.3, 15.0, 15.6, 15.7, 14.8, 14.5, 14.2, 14.9, 14.9, ...
    15.2, 15.0, 15.3, 15.6, 15.1, 14.9, 14.2, 14.6, 15.8, 15.2, ...
    15.9, 15.2, 15.0, 14.9, 14.8, 14.5, 15.1, 15.5, 15.5, 15.1, ...
    15.1, 15.0, 15.3, 14.7, 14.5, 15.5, 15.0, 14.7, 14.6, 14.2, ...
    ];

% 柯尔莫哥洛夫(Kolmogorov-Smirnov) 检验
pd = makedist('Normal', 'mu', 15.0780, 'sigma', 0.4325);
[h, p, st] = kstest(diameters, 'CDF', pd);

% 展示结果
h
p
st

% 画图展示
cdfplot(diameters)
hold on
x_values = linspace(min(diameters), max(diameters));
plot(x_values, normcdf(x_values, 15.0780, 0.4325), 'r-')
legend('Empirical CDF', 'Normal CDF', 'Location', 'best')

4.结果

image-20230410210937454

在结果中，我们可以看到，h的值为0，所以我们可以认为题目中的数据是服从题目中所给出的正态分布的。

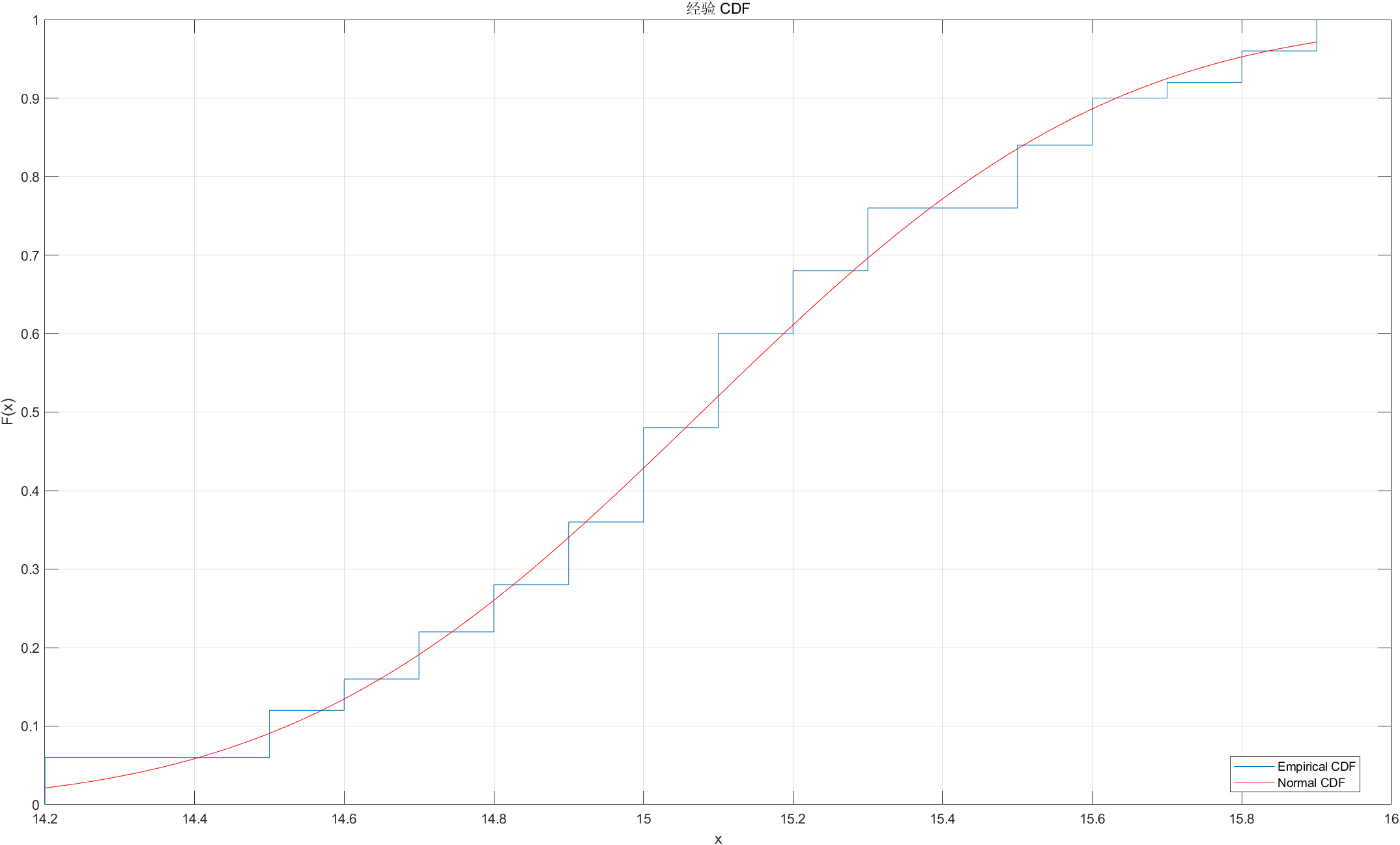
image-20230410211015252

同时，我还将经验累积分布函数和正态分布的累积分布函数绘制在同一个图形中，以便进行比较和分析。经过直观比较也可以看出数据服从正态分布。这与上面的kstest函数的计算结果相符合。

习题7.4

1. 题目要求

image-20230411154317389

2.解题过程

解：

原假设 $$ H_{0}:\mu_{1}=\mu_{2}=\mu_{3} \ H_{1}:\mu_{1},\mu_{2},\mu_{3}不全相等 $$ 如果H0为真： $$ F=\frac{\left(\,n\,-s\,\right)S_{A}}{\left(\,s\,-\,1\,\right)S_{E}}\sim F\left(\,s\,-\,1\,,n\,-\,s\,\right) $$ 拒绝域为 $$ F>F_{\alpha}(s-1\,,n-3\,)=F_{\alpha}(2\,,12\,)=3.8853 $$ 下面，直接使用anova1函数就可以解决问题。

3.程序

求解的MATLAB程序如下：

clc, clear

a = [98, 93, 103, 92, 110; ...
    100, 108, 118, 99, 111; ...
    129, 140, 108, 105, 116];

% 方差分析
[p,t,st] = anova1(a'); % 注意这里要转置一下

% 展示结果
p
t
st
F = t{2,5}

4.结果

image-20230411154911977

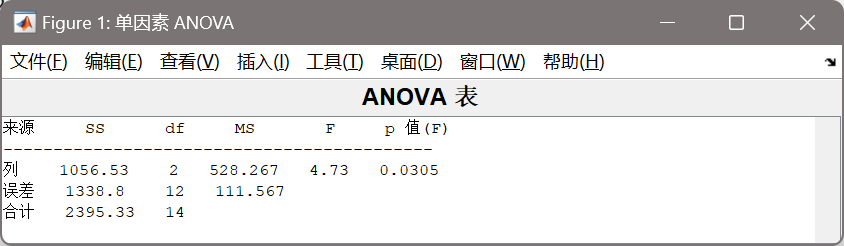
image-20230411154926885

通过上面的结果，我们可以看出： $$ S_A=1056.53\S_E=1338.8\F=4.7350 $$ 结果在拒绝域当中，所以认为，理赔额均值存在显著差异。