跳转至

第五讲-微分方程建模

习题6.4

1. 题目要求

image-20230329154221554

2.解题过程

解：

(1)

对函数值 \(s(t)\) 的影响因素，根据题目分析，可以得到如下两点：

  • 下降速度与 $ s(t)$ 的值的大小成正比，设比例系数为 \(\lambda\) ，所以式子中有一个部分为：$ -\lambda s(t) $ 。
  • 增长速度与 \(a(t)\) 的值的大小成正比，设比例系数为 \(\mu\) ，所以式子中有一个部分为：$ +\mu a(t) $ 。

但是，题目中说到，广告只能影响这种商品在市场上尚未饱和的部分(设饱和量为M)，所以有两个选择：分段函数 或者 渐进函数。

我选择使用渐进函数，渐近线为M，增长部分改为：\(\mu a(t)\left(1-\frac{s(t)}{M}\right)\) 。

这样，当 s=M 或者 a=0 时，销量都不会上涨，符合题意。

将所有分析合并，建立如下模型： $$ \frac{\mathrm{d} s}{\mathrm{d} t}=\mu a(t)\left(1-\frac{s(t)}{M}\right)-\lambda s(t) $$ (2)

广告宣传只进行有限时间 \(\tau\) ，且广告费为常数a，所以建立下列函数 $$ a(t)= \begin{cases}a/c, & 0<t \leqslant \tau, \ 0, & t \geqslant \tau . \end{cases} $$ 带入(1)中公式，并移项，有： $$ {\frac{\mathrm{d}s}{\mathrm{d}t}}+\left(\lambda\,+{\frac{\mu a}{M\tau}}\right)s\ ={\frac{\mu a}{\tau}},0\ <t<\tau, $$

(3)

先讨论 \(0<t \leqslant \tau\) :

为了运算方便，进行换元： $$ b = {\lambda\,+\,{\frac{\mu a}{M\tau}} , \,\,\, c={\frac{\mu a}{\tau}}}\ $$ 则上述式子化简为： $$ {\frac{\mathrm{d}s}{\mathrm{d}t}\,+\,b s\,=\,c\,,} $$ (4)

这是一个一阶非齐次线性微分方程.

假设初始值为 \(s_0\) ,可以得出结果为: $$ s(t)= \frac{c}{b}\left(1-\mathrm{e}^{-b t}\right)+s_{0} \mathrm{e}^{-b t}, & 0<t \leqslant \tau \ $$ (5)

再讨论 \(t \geqslant \tau\) :

式子为： $$ {\frac{\mathrm{d}s}{\mathrm{d}t}}=-\,\lambda s, $$ 可以得出结果为： $$ s(t)= s(\tau) \mathrm{e}^{\lambda(\tau-t)}, t \geqslant \tau . $$ (6)

合并所有结果，得到： $$ s(t)= \left{\begin{array}{ll}

\frac{c}{b}\left(1-\mathrm{e}^{-b t}\right)+s_{0} \mathrm{e}^{-b t}, & 0<t \leqslant \tau, \

s(\tau) \mathrm{e}^{\lambda(\tau-t)}, & t \geqslant \tau .

\end{array}\right. $$

3.结果

\(s(t)\) 的变化符合下列函数： $$ s(t)= \left{\begin{array}{ll}

\frac{c}{b}\left(1-\mathrm{e}^{-b t}\right)+s_{0} \mathrm{e}^{-b t}, & 0<t \leqslant \tau, \

s(\tau) \mathrm{e}^{\lambda(\tau-t)}, & t \geqslant \tau .

\end{array}\right. $$ 其中， $$ b = {\lambda\,+\,{\frac{\mu a}{M\tau}} , \,\,\, c={\frac{\mu a}{\tau}}}\ $$

习题6.5(1)

1. 题目要求

image-20230329185946579

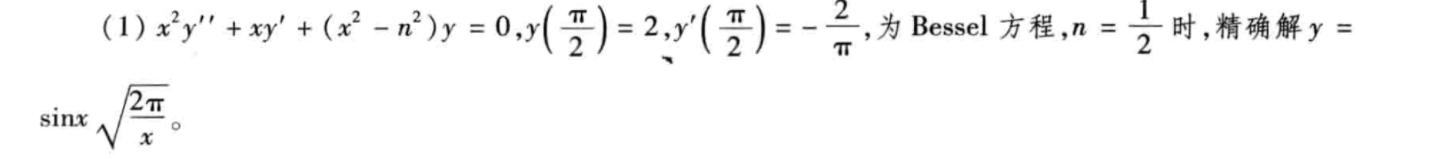
image-20230329190003552

2.解题过程

解：

Matlab的工具箱提供了几个解常微分方程的功能函数，如ode45 、ode23 、ode113 。其中，ode45 采用四五阶龙格库塔方法（以下简称RK方法），是解非刚性常微分方程的首选方法； ode23 采用二三阶龙格库塔方法。

高阶常微分方程，必须做变量替换， 化成一阶微分方程组，才能使用Matlab求数值解。

设 \(y_1=y,y_2=y^{\prime}\) ,则原式化为： $$ \left{\begin{array}{ll} y_{1}^{\prime}=y_{2}, & y_{1}\left(\frac{\pi}{2}\right)=2, \ y_{2}^{\prime}=\left(\frac{n^{2}}{x^{2}}-1\right) y_{1}-\frac{y_{2}}{x}, & y_{2}\left(\frac{\pi}{2}\right)=-\frac{2}{\pi} . \end{array}\right. $$

接下来就可以用ode45来解决相关问题。

3.程序

求解的MATLAB程序如下：

clc, clear

syms y(x) % 符号变量
dy = diff(y); % 一阶导
d2y = diff(dy); % 二阶导

% 为了分析比较，首先求解符号解
y = dsolve(x^2*d2y+x*dy+(x^2 - 1 / 4)*y, ...
    y(pi/2) == 2, dy(pi/2) == -2/pi); % 直接所有内容
y = simplify(y); % 化简结果
symdisp(y); % 直观输出函数（自建函数）
fplot(y); % 画图
hold on

%龙格库塔方法求解数值解
dy_2 = @(x, y) [y(2); (1 / 4 / x^x - 1) * y(1) - y(2) / x]; % 方程组的右端 注意：用分号隔开！！！

% 求解的区间是 [pi / 2, 15]
% 注意：2和-2/pi是区间左端点的时候的函数值，即x=pi/2时
[x, y] = ode45(dy_2, [pi / 2, 15], [2, -2 / pi]);
plot(x, y(:,1), '*'); % 画图 注意画的是y1

legend('符号解','数值解');

4.结果

微分方程求解结果如下：

image-20230329190441168

通过函数曲线可以看出，解析解和数值解吻合。

image-20230329190529596

习题6.5(2)

1. 题目要求

image-20230329185946579

image-20230329190838960

2.解题过程

解：

设 \(y_1=y,y_2=y^{\prime}\) ,则原式化为： $$ \left{\begin{array}{ll} y_{1}^{\prime}= \,y_{2}\,,&{{y_{1}(0)~=~1\,,}} \ y_{2}^{\prime}= -\,y_{1}\mathrm{cos}x\,,&y_{2}(0)~=\,0. \end{array}\right. $$ 接下来就可以用ode45来解决相关问题。

3.程序

求解的MATLAB程序如下：

clc, clear

% 使用幂级数解作为对照
power_series = @(x) 1 - 1 / gamma(3) * x.^2 + 2 / gamma(5) * x.^4 - 9 / gamma(7) * x.^6 + 55 / gamma(9) * x.^8;
x = 0:0.1:4;
y = power_series(x);
plot(x, y);
hold on

%龙格库塔方法求解数值解
dy = @(x, y) [y(2); -y(1) * cos(x)]; % 方程组的右端 注意：用分号隔开！！！

[x, y] = ode45(dy, [0, 4], [1, 0]);
plot(x, y(:, 1), '*'); % 画图 注意画的是y1

legend('幂级数解', '数值解');

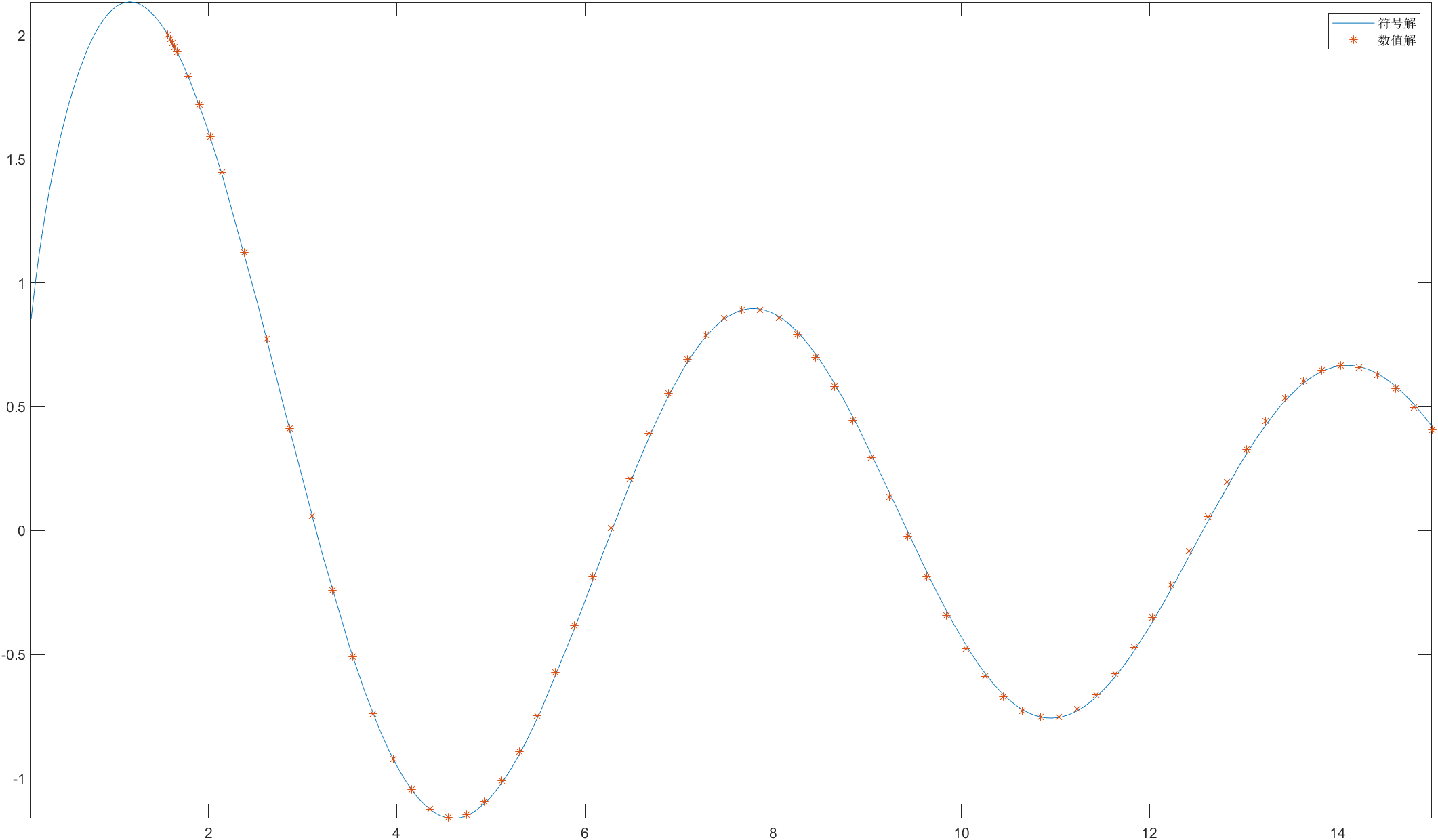
4.结果

通过函数曲线可以看出，当x较小的时候，级数解的近似值和数值解吻合较好。

image-20230329191458852

习题6.6

1. 题目要求

image-20230329191845404

2.第(1)问

解：

(1)

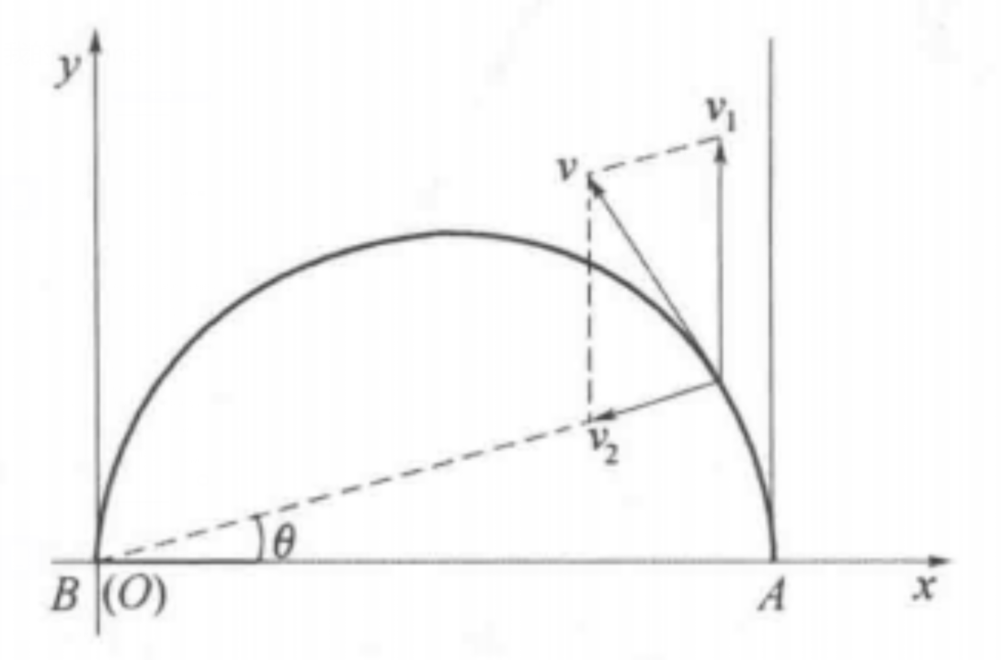
image-20230329193240726

如图建立坐标系。

我们可以看出，小船的和速度是水速和静水速度的向量和，其中，水速平行与河岸（y轴），静水速度始终朝向B点。

根据正交分解，我们可以求出x与y方向的速度： $$ {\frac{\mathrm{d}x}{\mathrm{d}t}}=-\,v_{2}\cos\theta\,,{\frac{\mathrm{d}y}{\mathrm{d}t}}=v_{1}-\,v_{2}\sin\theta. $$

根据几何关系，我们可以求出： $$ \cos\theta\,=\,{\frac{x}{\sqrt{x^{2}\,+\,y^{2}}}},\sin\theta\,=\,{\frac{y}{\sqrt{x^{2}\,+\,y^{2}}}}, $$ 联立（14）（15）式，得到： $$ {\frac{\mathrm{d}x}{\mathrm{d}t}}=-v_{2}\,{\frac{x}{\sqrt{x^{2}+y^{2}}}}\,,{\frac{\mathrm{d}y}{\mathrm{d}t}}=v_{1}-v_{2}\,{\frac{y}{\sqrt{x^{2}+y^{2}}}}, $$ 将（16）的两个式子相除，得到： $$ \frac{\mathrm{d}y}{\mathrm{d}x}=-\,k\,{\frac{{\sqrt{x^{2}+y^{2}}}}{x}}+{\frac{y}{x}},0<x<d $$ 这是一个一阶齐次微分方程，于是得到初值问题： $$ \left{\begin{array}{ll} {\frac{\mathrm{d}y}{\mathrm{d}x}}=-\,k\,{\frac{{\sqrt{x^{2}+y^{2}}}}{x}}+{\frac{y}{x}},0<x<d\ y(d)=0 \end{array}\right. $$ 为了求解这个微分方程，我试图使用Matlab的dsolve函数解决，但是matlab无法解决这个微分方程。

image-20230329204034471

使用Wolfram Mathematica软件的Dsolve函数，成功解出了微分方程的解为： $$ y\,=\,\frac{d}{2}\,\Bigl[\left(\frac{x}{d}\right)^{1-k}\,-\,\left(\frac{x}{d}\right)^{1+k}\,\Bigr],0<x<d. $$

3.第(2)问

根据第一问，可知参数方程为： $$ \left{\begin{array}{ll} {\frac{\mathrm{d}x}{\mathrm{d}t}}=-{\frac{2x}{\sqrt{x^{2}+y^{2}}}},x(0)=d\ {\frac{\mathrm{d}y}{\mathrm{d}t}}=1-{\frac{2y}{\sqrt{x^{2}+y^{2}}}},y(0)=0 \end{array}\right. $$ 求解的MATLAB程序如下：

clc, clear

d = 100;
v1 = 1;
v2 = 2;
k = 0.5;

% 第一问的解析解
y = @(x)d / 2 * ((x / d).^(1 - k) - (x / d).^(1 + k));
fplot(y, [0, 100]);
hold on

%龙格库塔方法求解数值解
dy = @(t, xy) [-2 * xy(1) / sqrt(xy(1)^2+xy(2)^2); 1 - 2 * xy(2) / sqrt(xy(1)^2+xy(2)^2)]; % 方程组的右端 注意：用分号隔开！！！

[t, xy] = ode45(dy, [0, 60], [100, 0]);
plot(xy(:, 1), xy(:, 2), '*'); % 画图 注意画的是y1

legend('符号解', '数值解');

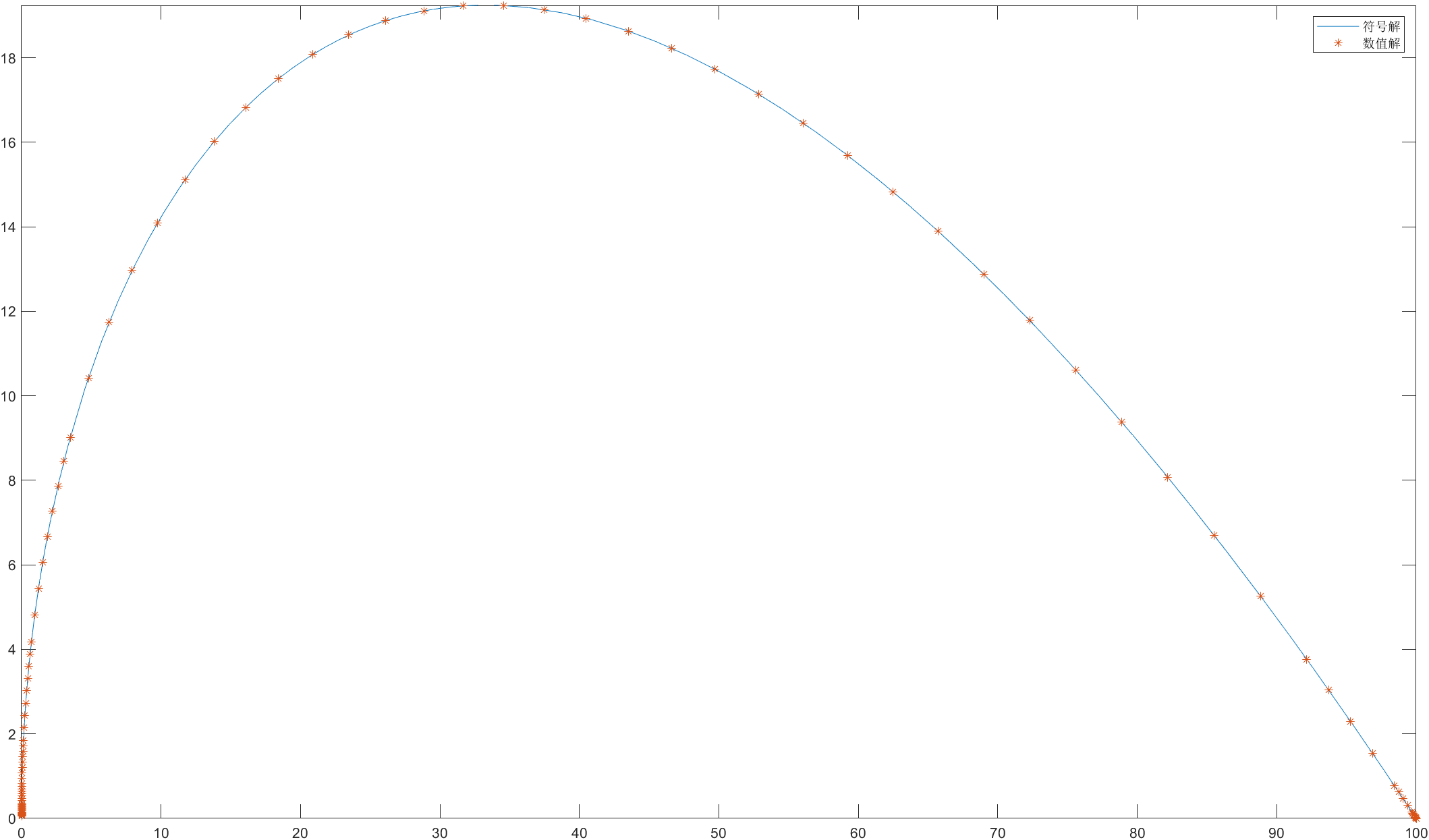
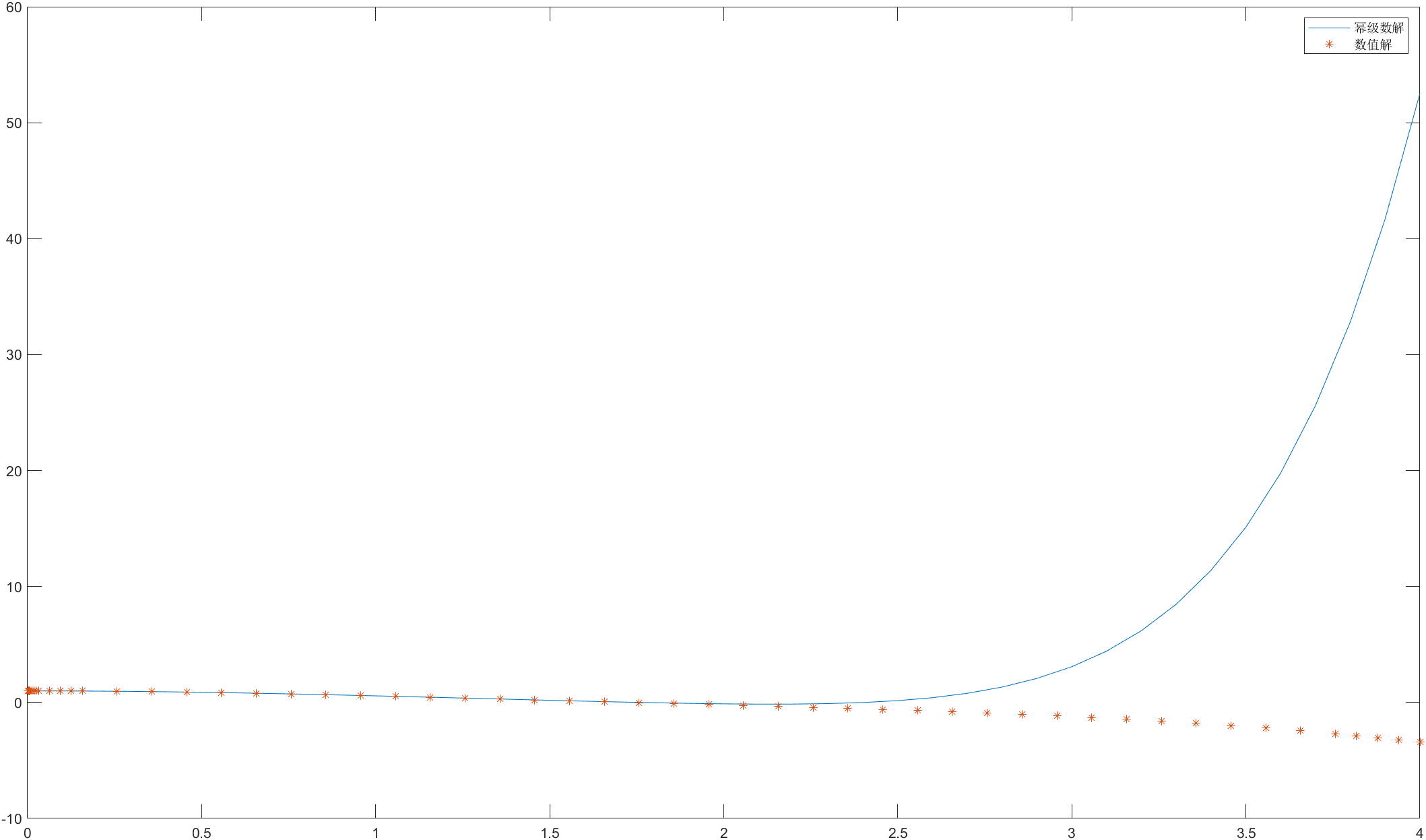
4.结果

渡河所需时间需要不断地尝试，修改处如下图所示：

image-20230329210036426

测试过程如下图（测试数据为40，很明显未到岸）：

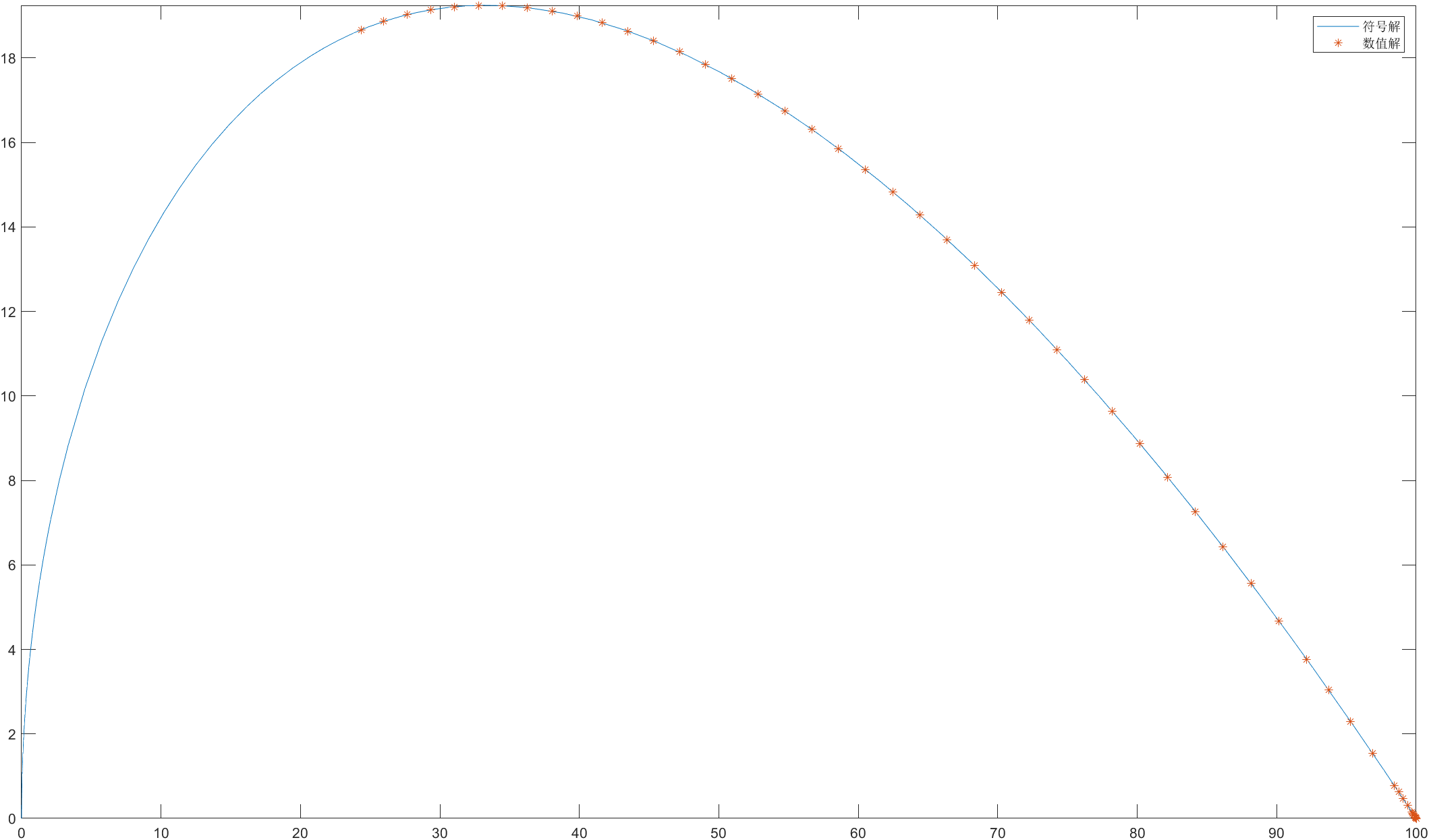
image-20230329210153081

最终，试验得到渡河所用时间为66.6秒，数值解与解析解的对照图（航行曲线）如下图：

image-20230329210414770