跳转至

第四讲-插值与拟合

习题5.2

1. 题目要求

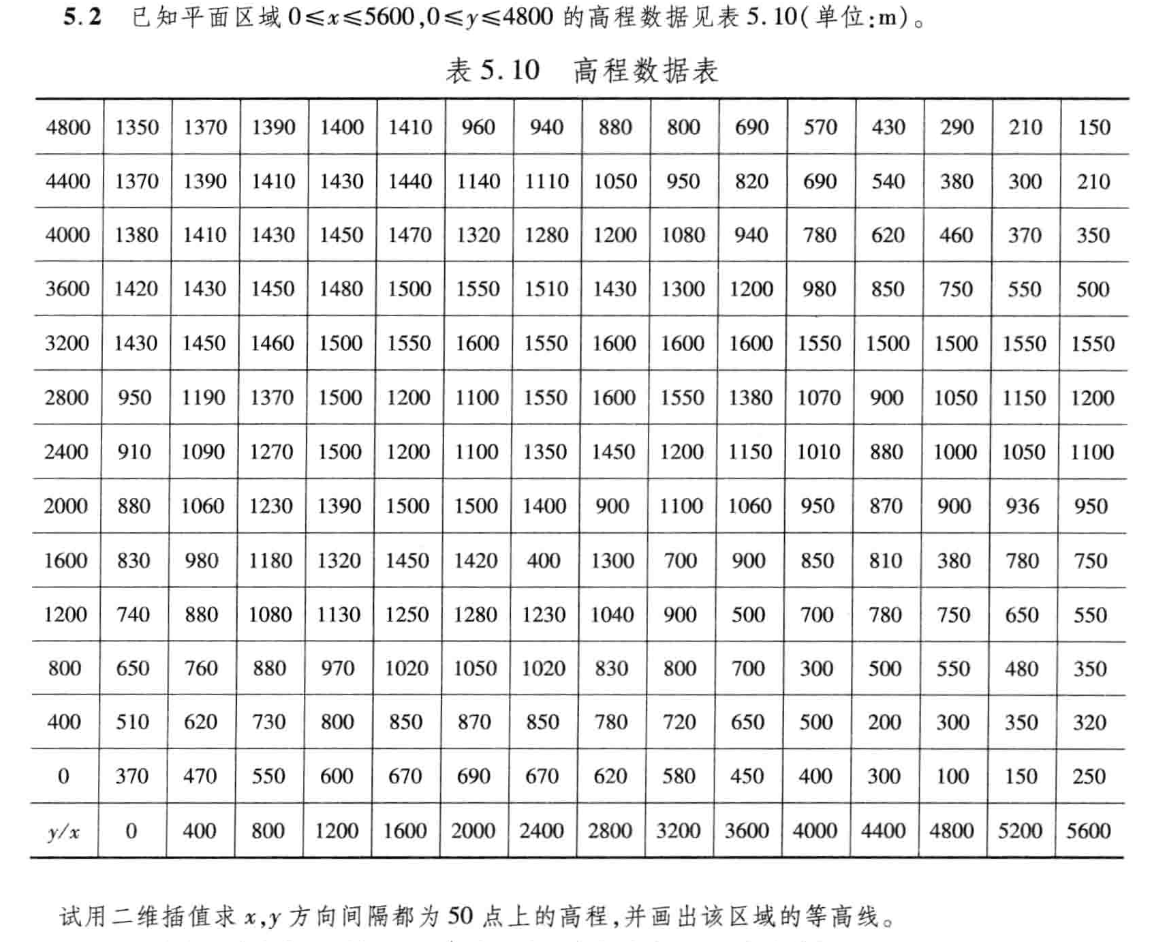
image-20230320204209894

2.解题过程

解：

这是一个典型的二维插值的问题。

有一点值得注意的是，题目的表格中，x与y的原点在左下角，并且正方向分别向右、向上。为了方便使用csape函数，我们需要的是行标为x、列标为y，原点在左上角，正方向分别向下、向右。

所以需要对数据矩阵进行先转置、再左右翻转的操作。

处理结果图下： $$ z_{input} = \begin{bmatrix} 370 & 510 & 650 & 740 & 830 & 880 & 910 & 950 & 1430 & 1420 & 1380 & 1370 & 1350\ 470 & 620 & 760 & 880 & 980 & 1060 & 1090 & 1190 & 1450 & 1430 & 1410 & 1390 & 1370\ 550 & 730 & 880 & 1080 & 1180 & 1230 & 1270 & 1370 & 1460 & 1450 & 1430 & 1410 & 1390\ 600 & 800 & 970 & 1130 & 1320 & 1390 & 1500 & 1500 & 1500 & 1480 & 1450 & 1430 & 1400\ 670 & 850 & 1020 & 1250 & 1450 & 1500 & 1200 & 1200 & 1550 & 1500 & 1470 & 1440 & 1410\ 690 & 870 & 1050 & 1280 & 1420 & 1500 & 1100 & 1100 & 1600 & 1550 & 1320 & 1140 & 960\ 670 & 850 & 1020 & 1230 & 400 & 1400 & 1350 & 1550 & 1550 & 1510 & 1280 & 1110 & 940\ 620 & 780 & 830 & 1040 & 1300 & 900 & 1450 & 1600 & 1600 & 1430 & 1200 & 1050 & 880\ 580 & 720 & 800 & 900 & 700 & 1100 & 1200 & 1550 & 1600 & 1300 & 1080 & 950 & 800\ 450 & 650 & 700 & 500 & 900 & 1060 & 1150 & 1380 & 1600 & 1200 & 940 & 820 & 690\ \vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots \end{bmatrix} $$ 接下来，使用csape和fnval函数进行三次样条插值。

最后，使用contourf展示等高线图。

3.程序

求解的MATLAB程序如下：

clc , clear

z_input = ...
    [ ...
    1350, 1370, 1390, 1400, 1410, 960, 940, 880, 800, 690, 570, 430, 290, 210, 150; ...
    1370, 1390, 1410, 1430, 1440, 1140, 1110, 1050, 950, 820, 690, 540, 380, 300, 210; ...
    1380, 1410, 1430, 1450, 1470, 1320, 1280, 1200, 1080, 940, 780, 620, 460, 370, 350; ...
    1420, 1430, 1450, 1480, 1500, 1550, 1510, 1430, 1300, 1200, 980, 850, 750, 550, 500; ...
    1430, 1450, 1460, 1500, 1550, 1600, 1550, 1600, 1600, 1600, 1550, 1500, 1500, 1550, 1550; ...
    950, 1190, 1370, 1500, 1200, 1100, 1550, 1600, 1550, 1380, 1070, 900, 1050, 1150, 1200; ...
    910, 1090, 1270, 1500, 1200, 1100, 1350, 1450, 1200, 1150, 1010, 880, 1000, 1050, 1100; ...
    880, 1060, 1230, 1390, 1500, 1500, 1400, 900, 1100, 1060, 950, 870, 900, 936, 950; ...
    830, 980, 1180, 1320, 1450, 1420, 400, 1300, 700, 900, 850, 810, 380, 780, 750; ...
    740, 880, 1080, 1130, 1250, 1280, 1230, 1040, 900, 500, 700, 780, 750, 650, 550; ...
    650, 760, 880, 970, 1020, 1050, 1020, 830, 800, 700, 300, 500, 550, 480, 350; ...
    510, 620, 730, 800, 850, 870, 850, 780, 720, 650, 500, 200, 300, 350, 320; ...
    370, 470, 550, 600, 670, 690, 670, 620, 580, 450, 400, 300, 100, 150, 250; ...
    ];

% 这个矩阵的x是列从左到右的方向，所以需要转置
z_input = z_input';
% y需要从小到大，把矩阵左右颠倒
z_input = fliplr(z_input);

x_input = 0:400:5600;
y_input = 0:400:4800;

% 三次样条插值
pp = csape({x_input, y_input}, z_input);

x = 0:50:5600;
y = 0:50:4800;
z = fnval(pp, {x, y});

% 展示等高线
graph = contourf(x,y,z',20);
clabel(graph);

4.结果

输出的等高线图如下：

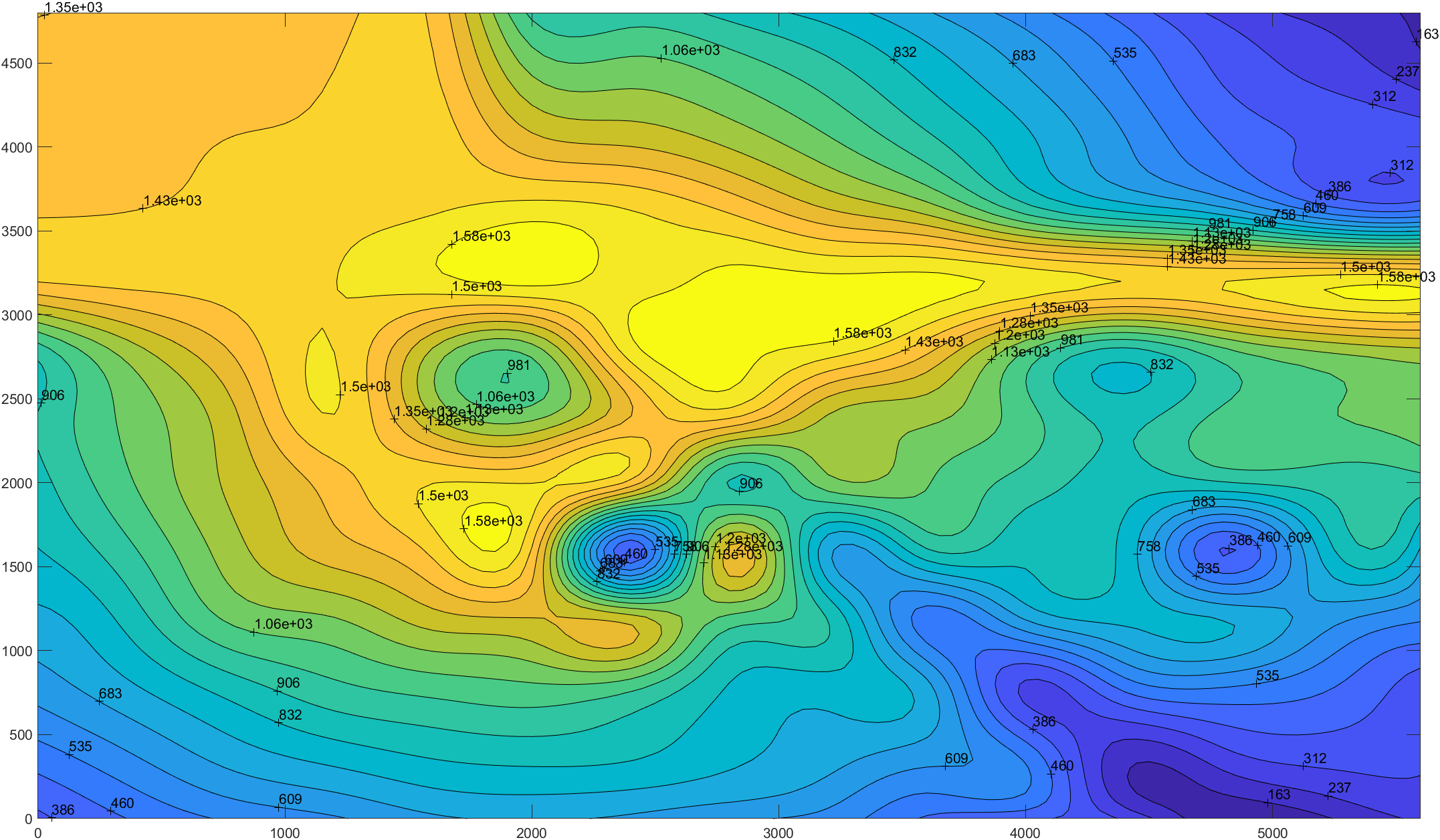
image-20230320211225222

本题成功使用二维插值求出了x,y方向间隔都为50点上的高程，存储在矩阵z当中。要想查询具体某点的高程，可以用鼠标在等高线图中点击，效果如下图。

image-20230321135159223

习题5.3

1. 题目要求

image-20230320211450947

2.解题过程

解：

本题思路较为简洁，使用lsqcurvefit函数进行最小二乘拟合，即可求出两个参数。

3.程序

求解的MATLAB程序如下：

clc, clear

x = 1:8;
y = [15.3, 20.5, 27.4, 36.6, 49.1, 65.6, 87.87, 117.6];

mf = @(cs, xdata) cs(1) * exp(cs(2)*xdata);

% cs:参数
cs = lsqcurvefit(mf, rand(2, 1), x, y);
cs

4.结果

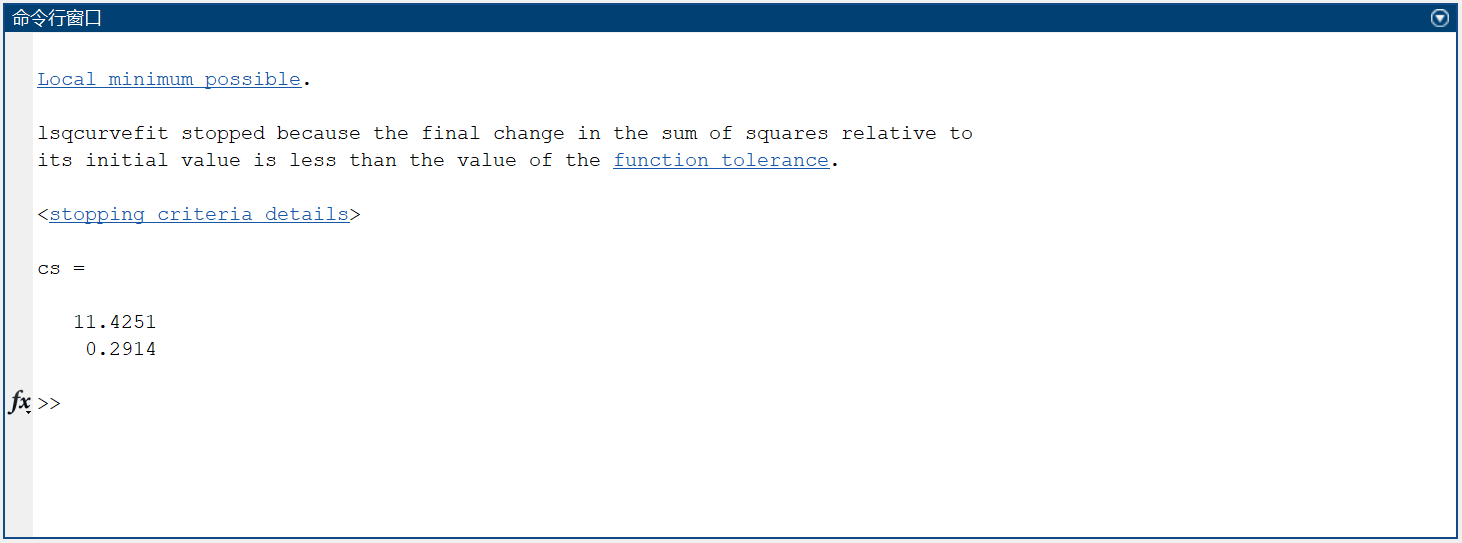
image-20230320212125760

求得参数a和b的估计值分别为：

\[ \hat{a}=11.43,\hat{b}=0.29 \]

拟合的函数为： $$ y=11.34e^{0.29x} $$

习题5.4

1. 题目要求

image-20230321133549683

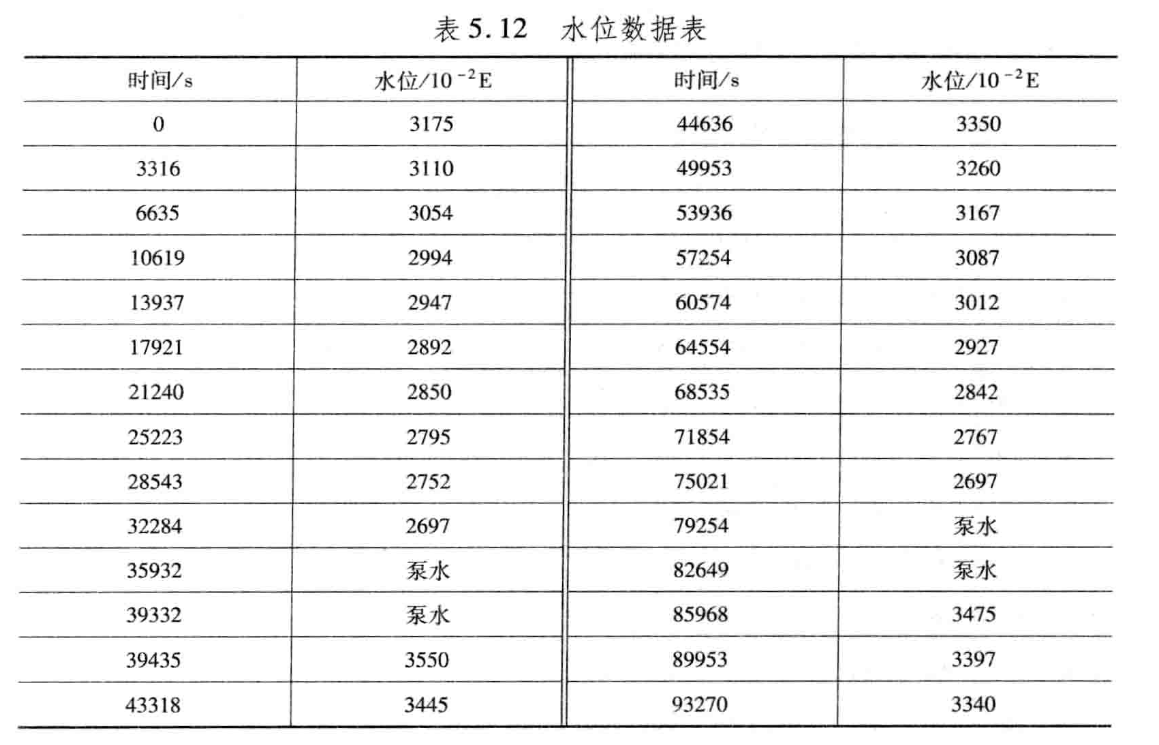
image-20230321133615120

2.解题过程

解：

本题考察的是用梯度和三次样条插值方法求解水箱水位变化对应的流出速度问题。

主要步骤如下：

  • 从表格中读取时间和水位的数据，并转换成米和小时为单位。
  • 计算水箱中水的体积，公式为V = pi / 4 * D * D * h，其中D是水箱的直径，h是水位高度。
  • 使用gradient函数计算体积对时间的变化率，这相当于对体积求导。体积的变化率等于流出速度的相反数。
  • 过滤掉任何负的流出速度值，这些是由于向水箱中泵水造成的。只保留正值和相应的时间点。
  • 使用csape函数创建一个以时间为自变量，流出速度为因变量的三次样条插值函数。这样可以平滑数据中的噪声或波动。
  • 使用ppval函数在更细密的时间间隔上评估插值函数，并在图上绘制原始数据点和插值曲线。

3.程序

求解的MATLAB程序如下：

clc, clear

% 写入表格中的所有数据，其中泵水的数据去除不用
t = [0, 3316, 6635, 10619, 13937, 17921, 21240, 25223, ...
    28543, 32284, 39435, 43318, 44636, 49953, 53936, 57254, ...
    60574, 64554, 68535, 71854, 75021, 85968, 89953, 93270];
h = [3175, 3110, 3054, 2994, 2947, 2892, 2850, 2795, 2752, ...
    2697, 3550, 3445, 3350, 3260, 3167, 3087, 3012, 2927, ...
    2842, 2767, 2697, 3475, 3397, 3340];

E = 0.3024; % 单位转换
D = 57 * E;
h = h / 100 * E;
t = t / 3600;
V = pi / 4 * D * D * h; % 计算体积

dV = gradient(V, t); % 对体积求导，就是体积的变化率
dV = -dV; % 流出流速的大小是体积变化率的相反数

% 流出速度一定是正的，但是在计算结果中出现了个别极端的负值
% 出现的原因是泵水的左右数据会受到泵水的影响
% 通过筛选，直接去除掉负的数值点，以及相对应的t
pos = dV.' > 0; 
dV = dV(pos);
t = t(pos);

% 三次插值
pp = csape(t, dV);

t_detail = 0:0.1:t(end);
fdV = ppval(pp, t_detail);

% 展示图表
hold on
plot(t, dV, '*') % 这是原始数据，用*描出来
plot(t_detail, fdV) % 这是曲线

% 求一下24小时流量
sum = trapz(t_detail(1:241),fdV(1:241)) % 通过观察，第241个数据点刚好是24小时

4.结果

f(t)函数曲线绘制如下：

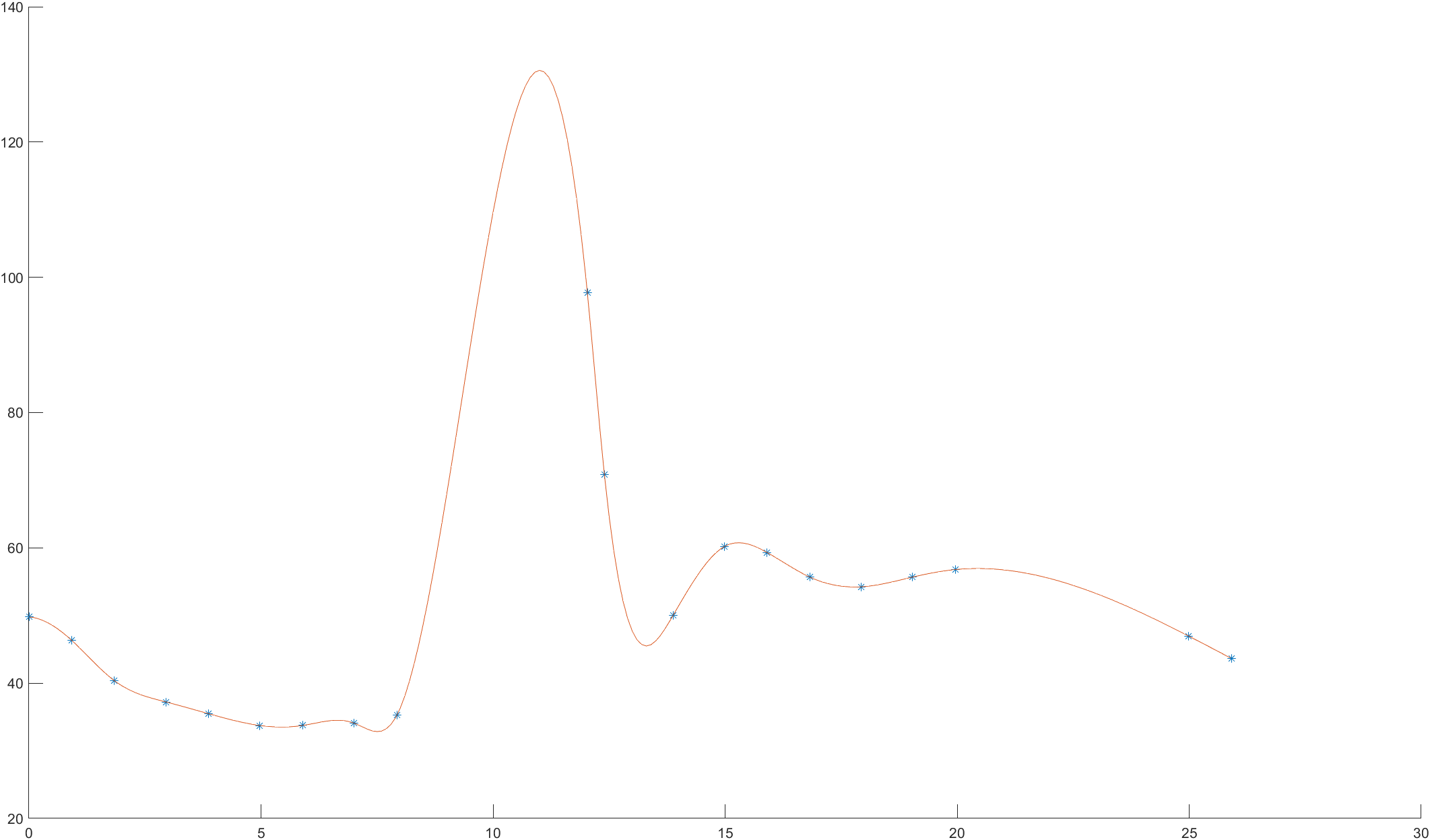
image-20230321134604588

要想查看在任意时刻t(包括水泵灌水期间)流出水箱的流量f(t)，可以用鼠标在图中点击，效果如下图：

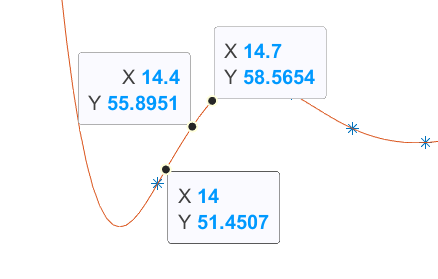
image-20230321135910157

此外，利用积分（通过观察，第241个数据点刚好是24小时，所以从1到241个数据点积分），可以求出24小时的总流量为1358立方米。