第三讲-非线性规划
习题3.1
1. 题目要求

2.解题过程
解:
设 第一季度生产x1台,第二季度生产x2台,第三季度生产x3台。
第一季度:费用全部为生产费用 $$ f_1=0.2x_1^2+50x_1 $$ 第二季度:费用为生产费用和存储费用 $$ f_2=0.2x_2^2+50x_2+4(x_1-40) $$ 第三季度:费用为生产费用和存储费用 $$ f_3=0.2x_2^3+50x_3+4(x_1+x_2-40-60) $$ 由题目所给数据可建立如下非线性规划模型: $$ \min f=0.2x_1^2+50x_1+0.2x_2^2+50x_2+4(x_1-40)+0.2x_2^3+50x_3+4(x_1+x_2-40-60) \\
\text { s. t. }\left\{
\begin{array}{l} x_{1} \geqslant 40 \\ x_{1}+x_{2} \geqslant 100 \\ x_{1}+x_{2}+x_{3} \geqslant 180 \\
x_{i} \geqslant 0, i=1,2,3
\end{array}\right. \\ $$
化成MATLAB标准型,即: $$ \min f= \frac{1}{2} \begin{bmatrix} x_1 & x_2 & x_3 \end{bmatrix} \begin{bmatrix} 0.4 & 0 & 0 \\ 0 & 0.4 & 0 \\ 0 & 0 & 0.4 \\ \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \\ x_3 \end{bmatrix} + \begin{bmatrix} 58 & 54 & 50 \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \\ x_3 \end{bmatrix} -560 \\
\text { s. t. }\left\{
\begin{array}{l}
\begin{bmatrix} 1 & 0 & 0 \\ 1 & 1 & 0 \\ 1 & 1 & 1 \\
\end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \\ x_3 \end{bmatrix} \geqslant \begin{bmatrix} 40 \\ 100 \\ 180 \end{bmatrix} \\
x_{i} \geqslant 0, i=1,2,3
\end{array}\right. \\ $$
3.程序
求解的MATLAB程序如下:
% 二次规划
clc , clear
H = 0.4 * eye(3); % 实对称矩阵
f = [58, 54, 50]; % 一次项
% 线性约束
A = [-1, 0, 0; ...
-1, -1, 0; ...
-1, -1, -1];
b = [-40, -100, -180];
%求解
[x, value] = quadprog(H, f, A, b, [], [], zeros(3, 1));
% 展示结果
x
value - 560
4.结果
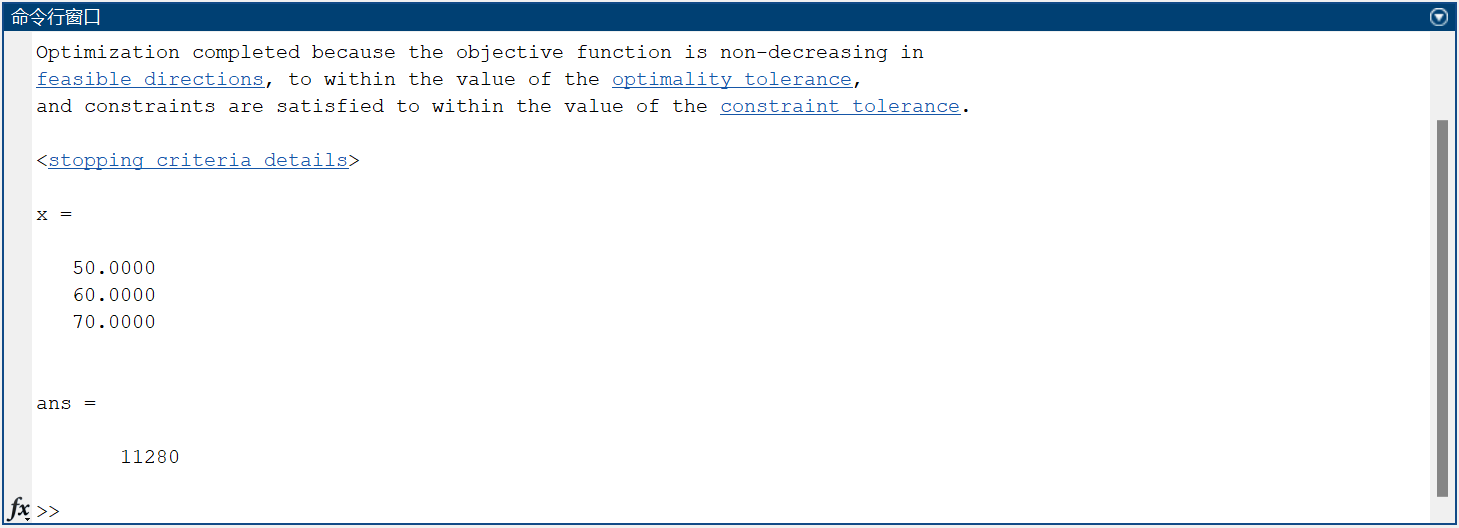
求得的最优解是:
第一季度生产50台,第二季度生产60台,第三季度生产70台。
最大利润:11280(元)
习题3.2
1. 题目要求
2.解题过程
解:
模型二中,建立如下非线性规划模型: $$ \min \sum_{i=1}^{6}\left(\Delta \theta_{i}\right)^{2}, \\
\text { s. t. }\left\{\begin{array}{l} \Delta_{i j}<0,1 \leqslant i \leqslant 5, i+1 \leqslant j \leqslant 6, \\ \left|\Delta \theta_{i}\right| \leqslant \frac{\pi}{6}, i=1,2, \cdots, 6 \text { 。 } \end{array}\right. $$ 其中: $$ \begin{array}{l} \Delta_{i j}=\tilde{b}{i j}^{2}-4 \tilde{a}{i j} \tilde{c}{i j}<0 \text { 。 } \\ \tilde{a}{i j}=4 \sin ^{2} \frac{\theta_{i}-\theta_{j}}{2}, \\ \tilde{b}{i j}=2 \left\{\left[x{i}(0)-x_{j}(0)\right]\left(\cos \theta_{i}-\cos \theta_{j}\right)+\left[y_{i}(0)-y_{j}(0)\right]\left(\sin \theta_{i}-\sin \theta_{j}\right)\right\}, \\ \tilde{c}{i j}=\left[x{i}(0)-x_{j}(0)\right]^{2}+\left[y_{i}(0)-y_{j}(0)\right]^{2}-64 。 \end{array} $$
3.程序
编写非线性约束函数
function [A, Aeq] = fun_A(x) % 变量是Theta的变化量
% 记录飞机初始数据
x0 = [150, 85, 150, 145, 130, 0]';
y0 = [140, 85, 155, 50, 150, 0]';
angle0 = [243, 236, 220.5, 159, 230, 52]';
angle = angle0 + x; % 初始角度加上角度的变化量:变化后的方向角
% 从现在开始,创建不等式约束,有ij嵌套循环
num = 1; % 计数
for i = 1:5
for j = i + 1:6
aij = 4 * (sind((angle(i) - angle(j))/2))^2;
bij = (x0(i) - x0(j)) * (cosd(angle(i)) - cosd(angle(j))) + (y0(i) - y0(j)) * (sind(angle(i)) - sind(angle(j)));
bij = bij * 2;
cij = (x0(i) - x0(j))^2 + (y0(i) - y0(j))^2 - 64;
A(num) = bij^2 - 4 * aij * cij;
num = num + 1;
end
end
Aeq = []; % 没有等式约束
end
编写目标函数
function f = fun_f(x) % 变量是Theta的变化量
f = sum(x.^2);
end
主程序
clc, clear
[theta, w] = fmincon('fun_f', rand(6, 1), [], [], [], [], -30*ones(6, 1), 30*ones(6, 1), 'fun_A');
theta
w
4.结果
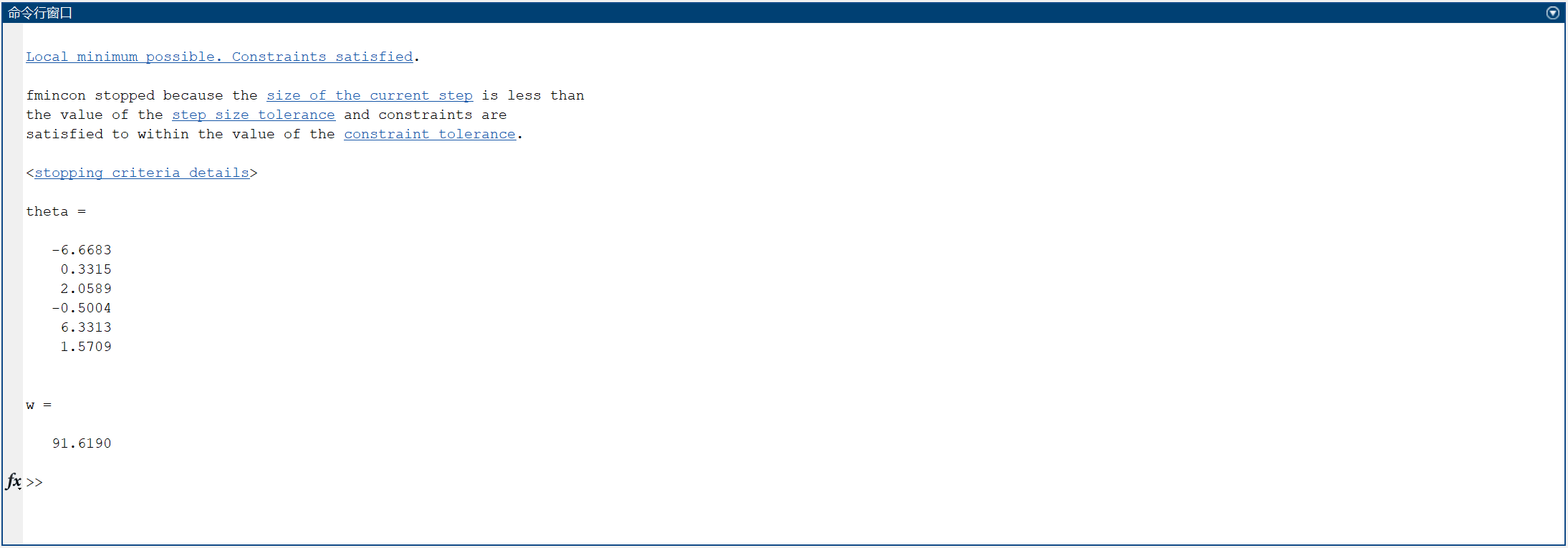
求得的最优解是:
习题3.3
1. 题目要求
2.解题过程
解:
模型二中,建立如下非线性规划模型: $$ \min \sum_{i=1}^{6}\left(\Delta \theta_{i}\right)^{2}, \\
\text { s. t. }\left\{\begin{array}{l} \Delta_{i j}<0,1 \leqslant i \leqslant 5, i+1 \leqslant j \leqslant 6, \\ \left|\Delta \theta_{i}\right| \leqslant \frac{\pi}{6}, i=1,2, \cdots, 6 \text { 。 } \end{array}\right. $$ 其中: $$ \begin{array}{l} \Delta_{i j}=\tilde{b}{i j}^{2}-4 \tilde{a}{i j} \tilde{c}{i j}<0 \text { 。 } \\ \tilde{a}{i j}=4 \sin ^{2} \frac{\theta_{i}-\theta_{j}}{2}, \\ \tilde{b}{i j}=2 \left\{\left[x{i}(0)-x_{j}(0)\right]\left(\cos \theta_{i}-\cos \theta_{j}\right)+\left[y_{i}(0)-y_{j}(0)\right]\left(\sin \theta_{i}-\sin \theta_{j}\right)\right\}, \\ \tilde{c}{i j}=\left[x{i}(0)-x_{j}(0)\right]^{2}+\left[y_{i}(0)-y_{j}(0)\right]^{2}-64 。 \end{array} $$ 罚函数为: $$ P(\boldsymbol{\theta}, M)=\sum_{i=1}^{6}\left(\Delta \theta_{i}\right)^{2}+M \sum_{i=1}^{r} \max \left(\Delta_{i j}, 0\right) $$
3.程序
编写罚函数
function P = penalty_function(x)
M = 1000000;
f = sum(x.^2);
% 记录飞机初始数据
x0 = [150, 85, 150, 145, 130, 0]';
y0 = [140, 85, 155, 50, 150, 0]';
angle0 = [243, 236, 220.5, 159, 230, 52]';
angle = angle0 + x; % 初始角度加上角度的变化量:变化后的方向角
% 从现在开始,创建g,有ij嵌套循环
num = 1; % 计数
for i = 1:5
for j = i + 1:6
aij = 4 * (sind((angle(i) - angle(j))/2))^2;
bij = (x0(i) - x0(j)) * (cosd(angle(i)) - cosd(angle(j))) + (y0(i) - y0(j)) * (sind(angle(i)) - sind(angle(j)));
bij = bij * 2;
cij = (x0(i) - x0(j))^2 + (y0(i) - y0(j))^2 - 64;
g(num) = bij^2 - 4 * aij * cij;
num = num + 1;
end
end
P = f + M * max([g, 0]);
end
主程序
clc, clear
[theta,w]=fminsearch('penalty_function',rand(6,1));
theta
w
4.结果

求得的最优解是:
习题3.4
1.题目要求

2.解题过程
解:
化成MATLAB标准型,即: $$ \min w=(-1)*[ \begin{bmatrix}3 & 1 & 0 \end{bmatrix} \begin{bmatrix} x_1^2 \\ x_2^2 \\ x_3^2 \end{bmatrix} + \begin{bmatrix} 2 & 3 & 1 \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \\ x_3 \end{bmatrix} ]\\
\text { s. t. }\left\{
\begin{array}{l}
\begin{bmatrix}2 & 2 & 0 \end{bmatrix} \begin{bmatrix} x_1^2 \\ x_2^2 \\ x_3^2 \end{bmatrix} + \begin{bmatrix} 1 & 1 & 1 \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \\ x_3 \end{bmatrix} -10 \leqslant 0 \\
\begin{bmatrix}1 & 1 & 0 \end{bmatrix} \begin{bmatrix} x_1^2 \\ x_2^2 \\ x_3^2 \end{bmatrix} + \begin{bmatrix} 1 & 1 & -1 \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \\ x_3 \end{bmatrix} -50 \leqslant 0 \\
\begin{bmatrix}1 & 0 & 0 \end{bmatrix} \begin{bmatrix} x_1^2 \\ x_2^2 \\ x_3^2 \end{bmatrix} + \begin{bmatrix} 2 & 2 & 1 \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \\ x_3 \end{bmatrix} -40 \leqslant 0 \\
\begin{bmatrix}1 & 0 & 0 \end{bmatrix} \begin{bmatrix} x_1^2 \\ x_2^2 \\ x_3^2 \end{bmatrix} + \begin{bmatrix} 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \\ x_3 \end{bmatrix} -2 = 0 \\
\begin{bmatrix} -1 & -2 & 0 \\ -1 & 1 & 0 \\ \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \end{bmatrix} \geqslant \begin{bmatrix} -1 \\ 0 \end{bmatrix} \\
\\ x_{1} \geqslant 0
\end{array}\right. \\ $$
3.程序
编写目标函数
function f = fun_f(x)
f = [3, 1, 0] * (x.^2) + [2, 3, 1] * x;
f = -f;
end
编写非线性约束函数
function [A, Aeq] = fun_A(x)
A = [[2, 2, 0] * (x.^2) + [1, 1, 1] * x - 10; ...
[1, 1, 0] * (x.^2) + [1, 1, -1] * x - 50; ...
[1, 0, 0] * (x.^2) + [2, 2, 1] * x - 40];
Aeq = [1, 0, 0] * (x.^2) + [0, 0, 1] * x - 2;
end
主程序
clc, clear
A = [-1, -2, 0; ...
-1, 0, 0];
b = [-1, 0];
[x, w] = fmincon('fun_f', rand(3, 1), A, b, [], [], [], [], 'fun_A');
x
w = -w
4.结果
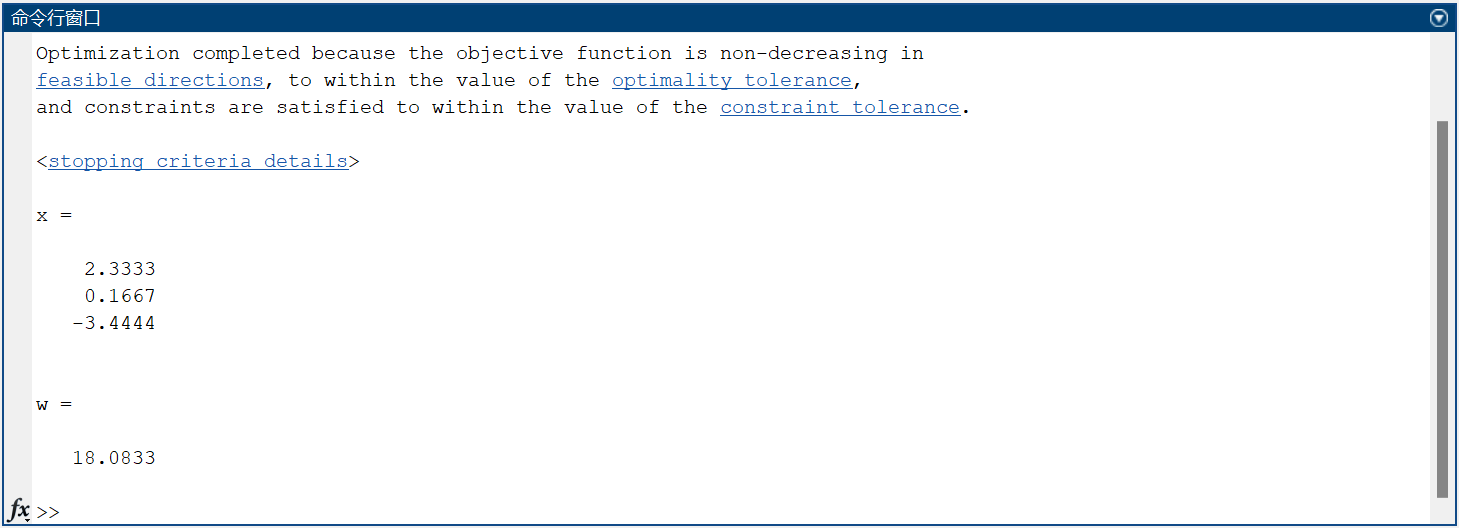
求得的最优解是: