第二讲-线性规划
习题1.3
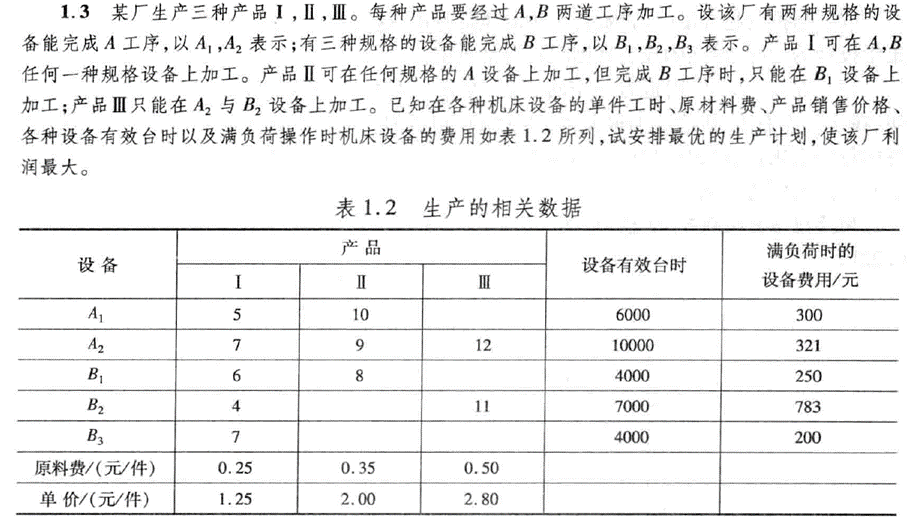
1. 题目要求
2.解题过程
解:
设 使用设备A1生产产品1:x1件,使用设备A2生产产品1:x2件,使用设备B1生产产品1:x3件,使用设备B2生产产品1:x4件,使用设备B3生产产品1:x5件,使用设备A1生产产品2:x6件,使用设备A2生产产品2:x7件,使用设备B1生产产品2:x8件,使用设备A1(B1)生产产品3:x9件。
梳理如下:
- 产品1:设备A1生产x1件,设备A2生产x2件,设备B1生产x3件,设备B2生产x4件,设备B3生产x5件
- 产品2:设备A1生产x6件,设备A2生产x7件,设备B1生产x8件
- 产品3:设备A1和B1共同生产x9件
值得注意的是,上述所有变量都是整数。
由题目所给数据可建立如下线性规划模型:
$$ \max w=(1.25-0.25)\times\left(x_{1}+x_{2}\right)+(2-0.35)\times\left(x_{6}+x_{7}\right)+(2.8-0.5)\times x_{9} \ -\frac{300}{6000}\times\left(5 x_{1}+10 x_{6}\right)-\frac{321}{10000}\times\left(7 x_{2}+9 x_{7}+12 x_{9}\right) \ -\frac{250}{4000}\times\left(6 x_{3}+8 x_{8}\right)-\frac{783}{7000}\times\left(4 x_{4}+11 x_{9}\right)-\frac{200}{4000} \times 7 x_{5} \
\text { s. t. }\left{
\begin{array}{l} 5 x_{1}+10 x_{6} \leqslant 6000 \ 7 x_{2}+9 x_{7}+12 x_{9} \leqslant 10 \ 6 x_{3}+8 x_{8} \leqslant 4000 \ 4 x_{4}+11 x_{9} \leqslant 7000, \ 7 x_{5} \leqslant 4000, \ x_{1}+x_{2}=x_{3}+x_{4}+x_{5} \ x_{6}+x_{7}=x_{8} \ x_{i} \geqslant 0, i=1,2, \cdots, 9
\end{array}\right. \ $$
化成MATLAB标准型,即: $$ \min w=(-1)*[(1.25-0.25)\times\left(x_{1}+x_{2}\right)+(2-0.35)\times\left(x_{6}+x_{7}\right)+(2.8-0.5)\times x_{9} \ -\frac{300}{6000}\times\left(5 x_{1}+10 x_{6}\right)-\frac{321}{10000}\times\left(7 x_{2}+9 x_{7}+12 x_{9}\right) \ -\frac{250}{4000}\times\left(6 x_{3}+8 x_{8}\right)-\frac{783}{7000}\times\left(4 x_{4}+11 x_{9}\right)-\frac{200}{4000} \times 7 x_{5}] \
\text { s. t. }\left{
\begin{array}{l}
\begin{bmatrix} 5 & 0 & 0 & 0 & 0 & 10 & 0 & 0 & 0\ 0 & 7 & 0 & 0 & 0 & 0 & 9 & 0 & 12\ 0 & 0 & 6 & 0 & 0 & 0 & 0 & 8 & 0\ 0 & 0 & 0 & 4 & 0 & 0 & 0 & 0 & 11\ 0 & 0 & 0 & 0 & 7 & 0 & 0 & 0 & 0\ \end{bmatrix} \begin{bmatrix} x_1 \ x_2 \ x_3 \ x_4 \ x_5 \ x_6 \ x_7 \ x_8 \ x_9 \ \end{bmatrix} \leqslant \begin{bmatrix} 6000 \ 10000 \ 4000 \ 7000 \ 4000 \end{bmatrix} \
\begin{bmatrix} 1 & 1 & -1 & -1 & -1 & 0 & 0 & 0 & 0 \ 0 & 0 & 0 & 0 & 0 & 1 & 1 & -1 & 0 \end{bmatrix} \begin{bmatrix} x_1 \ x_2 \ x_3 \ x_4 \ x_5 \ x_6 \ x_7 \ x_8 \ x_9 \ \end{bmatrix} = \begin{bmatrix} 0 \ 0 \end{bmatrix} \
x_{i} \geqslant 0, i=1,2, \cdots, 9
\end{array}\right. \ $$
3.程序
求解的MATLAB程序如下:
clc , clear
% pr:profit 每个产品的净利润
pr1 = 1.25 - 0.25;
pr2 = 2 - 0.35;
pr3 = 2.8 - 0.5;
pr = [pr1 * ones(1, 2), zeros(1, 3), pr2 * ones(1, 2), 0, pr3]; % 利润矩阵
% ec:equipment cost 每个设备的单位运行费用
ec1 = 300 / 6000;
ec2 = 321 / 10000;
ec3 = 250 / 4000;
ec4 = 783 / 7000;
ec5 = 200 / 4000;
ec = [5 * ec1, 7 * ec2, 6 * ec3, 4 * ec4, 7 * ec5, 10 * ec1, 9 * ec2, 8 * ec3, 12 * ec2 + 11 * ec4]; % 设备费用矩阵
% 易错:注意这里要乘以运行时长!
f = pr - ec; % 计算出销售利润与机器成本的和矩阵,也就是最终收益
f = -f; % 求min
A = [5, 0, 0, 0, 0, 10, 0, 0, 0; ...
0, 7, 0, 0, 0, 0, 9, 0, 12; ...
0, 0, 6, 0, 0, 0, 0, 8, 0; ...
0, 0, 0, 4, 0, 0, 0, 0, 11; ...
0, 0, 0, 0, 7, 0, 0, 0, 0];
b = [6000, 10000, 4000, 7000, 4000];
Aeq = [1, 1, -1, -1, -1, 0, 0, 0, 0; ...
0, 0, 0, 0, 0, 1, 1, -1, 0];
beq = zeros(2, 1);
intcon = 1:9;
[x, w] = intlinprog(f, intcon, A, b, Aeq, beq, zeros(9, 1));
w = -w; % 求max
% 输出结果
format shortG;
x
w
4.结果

求得的最优解是:
使用设备A1生产产品1:1200件,使用设备A2生产产品1:230件,使用设备B1生产产品1:0件,使用设备B2生产产品1:859件,使用设备B3生产产品1:571件,使用设备A1生产产品2:0件,使用设备A2生产产品2:500件,使用设备B1生产产品2:500件,使用设备A1和B1生产产品3:324件。
最大利润:1146.4(元)
习题1.4
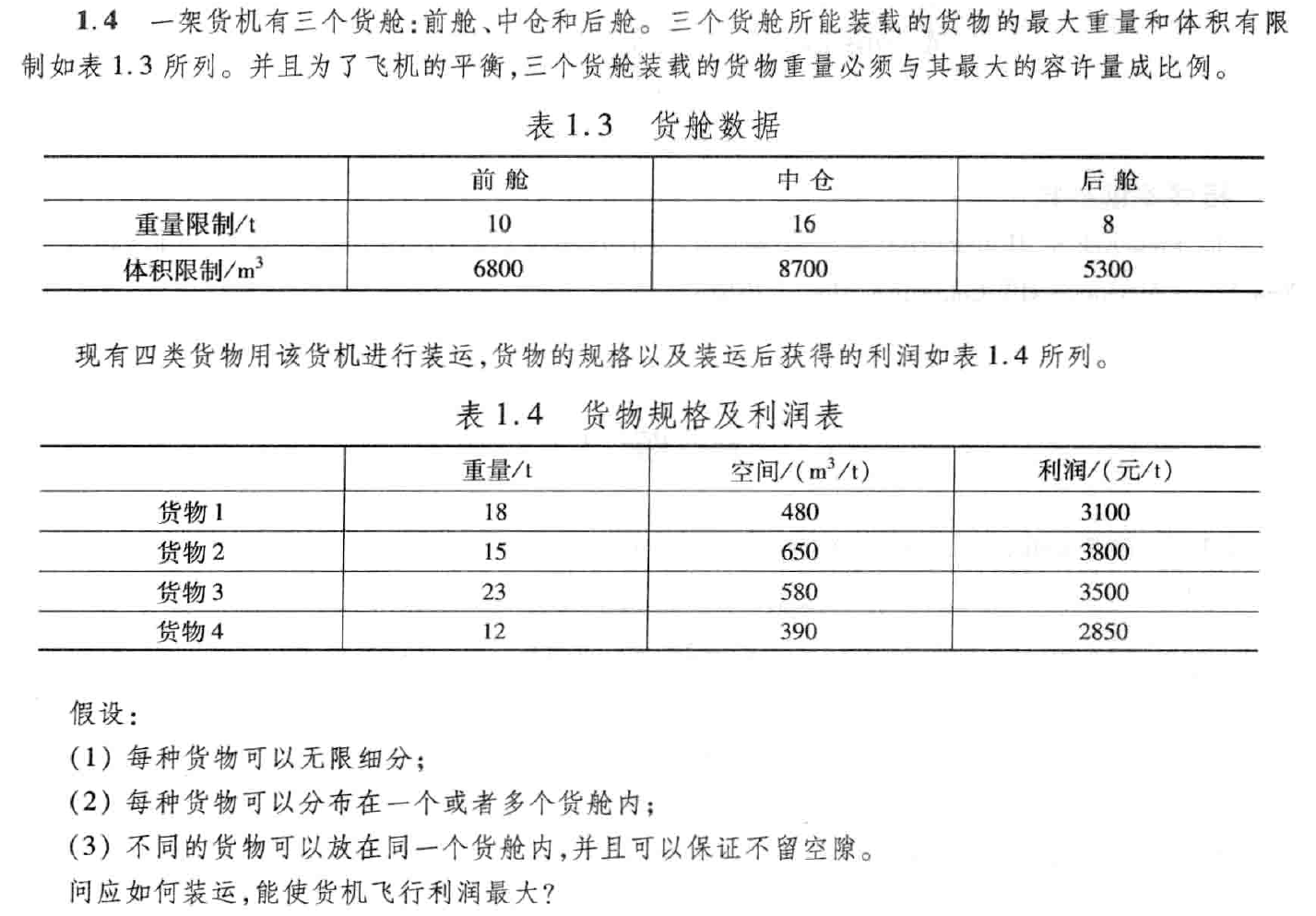
1.题目要求
2.解题过程
解:
设 前舱装运货物1:x1吨,前舱装运货物2:x2吨,前舱装运货物3:x3吨,前舱装运货物4:x4吨
中舱装运货物1:x5吨,中舱装运货物2:x6吨,中舱装运货物3:x7吨,中舱装运货物4:x8吨
后舱装运货物1:x9吨,后舱装运货物2:x10吨,后舱装运货物3:x11吨,后舱装运货物4:x12吨
由题目所给数据可建立如下线性规划模型: $$ \max w=3100\times\left(x_{1}+x_{5}+x_{9}\right)+3800\times\left(x_{2}+x_{6}+x_{10}\right)+3500\times \left(x_{3}+x_{7}+x_{11}\right)+2850\times\left(x_{4}+x_{8}+x_{12}\right) \
\text { s. t. }\left{
\begin{array}{l}
x_{1}+ x_{5}+x_{9} \leqslant 18 \ x_{2}+ x_{6}+x_{10} \leqslant 15 \ x_{3}+ x_{7}+x_{11} \leqslant 23 \ x_{4}+ x_{8}+x_{12} \leqslant 10 \
x_{1}+ x_{2}+x_{3}+ x_{4} \leqslant 10 \ x_{5}+ x_{6}+x_{7}+ x_{8} \leqslant 16 \ x_{9}+ x_{10}+x_{11}+ x_{12} \leqslant 8 \
480x_{1}+ 650x_{2}+580x_{3}+ 390x_{4} \leqslant 6800 \ 480x_{5}+ 650x_{6}+580x_{7}+ 390x_{8} \leqslant 8700 \ 480x_{9}+ 650x_{10}+580x_{11}+ 390x_{12} \leqslant 5300 \
16(x_{1}+ x_{2}+x_{3}+ x_{4})=10(x_{5}+ x_{6}+x_{7}+ x_{8})\ 8(x_{5}+ x_{6}+x_{7}+ x_{8})=16(x_{9}+ x_{10}+x_{11}+ x_{12})\
x_{i} \geqslant 0, i=1,2, \cdots, 12
\end{array}\right. \ $$ 化成MATLAB标准型,即: $$ \min w=(-1)*[3100\times\left(x_{1}+x_{5}+x_{9}\right)+3800\times\left(x_{2}+x_{6}+x_{10}\right)+3500\times \left(x_{3}+x_{7}+x_{11}\right)+2850\times\left(x_{4}+x_{8}+x_{12}\right) ]\
\text { s. t. }\left{
\begin{array}{l}
\begin{bmatrix} 1 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \ 0 & 1 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 1 & 0 & 0 \ 0 & 0 & 1 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 1 & 0 \ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 1 \ 1 & 1 & 1 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \ 0 & 0 & 0 & 0 & 1 & 1 & 1 & 1 & 0 & 0 & 0 & 0 \ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 1 & 1 & 1 \ 480 & 650 & 580 & 390 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \ 0 & 0 & 0 & 0 & 480 & 650 & 580 & 390 & 0 & 0 & 0 & 0 \ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 480 & 650 & 580 & 390 \end{bmatrix} \begin{bmatrix} x_1 \ x_2 \ x_3 \ x_4 \ x_5 \ x_6 \ x_7 \ x_8 \ x_9 \x_{10} \ x_{11} \ x_{12} \end{bmatrix} \leqslant \begin{bmatrix} 18 \ 15 \ 23 \ 12 \ 10 \ 16 \ 8 \ 6800 \ 8700 \ 5300 \end{bmatrix} \
\begin{bmatrix} 8 & 8 & 8 & 8 & -5 & -5 & -5 & -5 & 0 & 0 & 0 & 0 \ 0 & 0 & 0 & 0 & 1 & 1 & 1 & 1 & -2 & -2 & -2 & -2 \ \end{bmatrix} \begin{bmatrix} x_1 \ x_2 \ x_3 \ x_4 \ x_5 \ x_6 \ x_7 \ x_8 \ x_9 \x_{10} \ x_{11} \ x_{12} \end{bmatrix} = \begin{bmatrix} 0 \ 0 \end{bmatrix} \
x_{i} \geqslant 0, i=1,2, \cdots, 12
\end{array}\right. \ $$
3.程序
clc , clear
% 按行展开获得f
f = [3100 * ones(3, 1), 3800 * ones(3, 1), 3500 * ones(3, 1), 2850 * ones(3, 1)];
f = f';
f = f(:)';
f = -f; % 求min
A1 = [eye(4), eye(4), eye(4)];
A2 = blkdiag(ones(1, 4), ones(1, 4), ones(1, 4));
A3 = blkdiag([480, 650, 580, 390], [480, 650, 580, 390], [480, 650, 580, 390]);
A = vertcat(A1, A2, A3);
b = [18, 15, 23, 12, 10, 16, 8, 6800, 8700, 5300];
Aeq1 = [8 * ones(1, 4), -5 * ones(1, 4), zeros(1, 4)];
Aeq2 = [zeros(1, 4), ones(1, 4), -2 * ones(1, 4)];
Aeq = vertcat(Aeq1, Aeq2);
beq = zeros(2, 1);
% 获得结果
[x, w] = linprog(f, A, b, Aeq, beq, zeros(12, 1));
format longG;
% 转化为3*4的矩阵
x = reshape(x, [4, 3])'
% 求和
x = sum(x)
% 利润
w = -w % 求max
4.结果
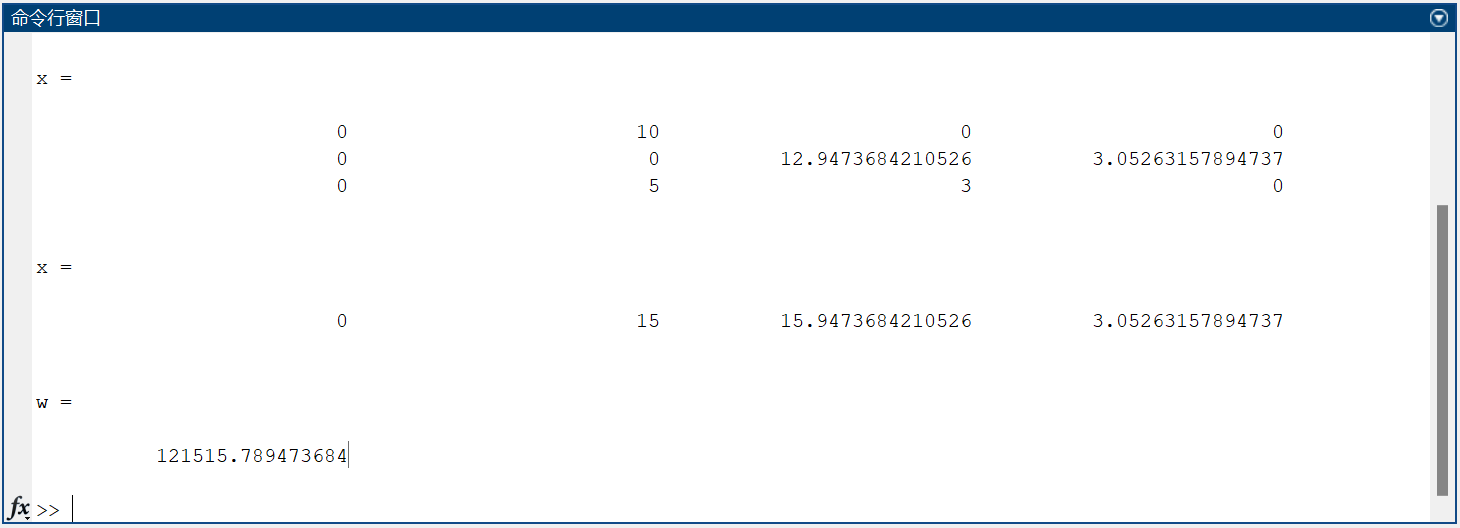
求得的最优解是:
前舱装运货物1:x1 = 0 吨 前舱装运货物2:x2 = 10.0000 吨 前舱装运货物3:x3 = 0 吨 前舱装运货物4:x4 = 0 吨
中舱装运货物1:x5 = 0 吨 中舱装运货物2:x6 = 0 吨 中舱装运货物3:x7 = 12.9474 吨 中舱装运货物4:x8 = 3.0526 吨
后舱装运货物1:x9 = 0 吨 后舱装运货物2:x10 = 5.0000 吨 后舱装运货物3:x11 = 3.0000 吨 后舱装运货物4:x12 = 0 吨
货物1的总装运量:x1 + x5 + x9 = 0 + 0 + 0 = 0 吨
货物2的总装运量:x2 + x6 + x10 = 10.0000 + 0 + 5.0000 = 15.0000 吨
货物3的总装运量:x3 + x7 + x11 = 0 + 12.9474 + 3.0000 = 15.9474 吨
货物4的总装运量:x4 + x8 + x12 = 0 + 3.0526 + 0 = 3.0526 吨
最大利润:121515.789(元)