第十三讲-相关分析
习题10.4
1. 题目要求
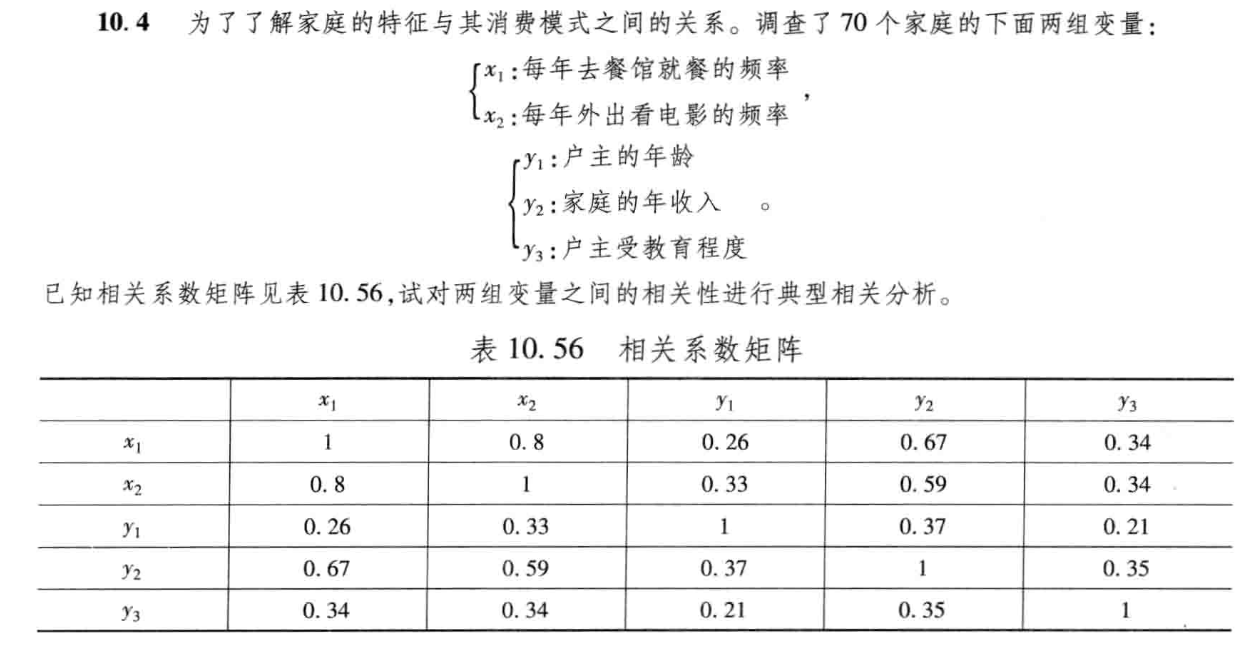
2.解题过程
解:
- 根据计算,我们得到了 \(\mathbf{X}\) 组的典型变量为: $$ u_1=0.7689x_1+0.2721x_2 $$
$$ u_2=-1.4787x_1+1.6443x_2 $$
- 我们也得到了原始变量与 \(\mathbf{X}\) 组典型变量之间的相关系数(如表 1)、原始变量与 \(\mathbf{Y}\) 组典型变量之间的相关系数(如表 2),以及两组典型变量之间的典型相关系数(如表 3)。
表 1:原始变量与 X 组典型变量之间的相关系数
| \(x_{1}\) | \(x_{2}\) | \(y_{1}\) | \(y_{2}\) | \(y_{3}\) | |
|---|---|---|---|---|---|
| \(u_{1}\) | 0.986586 | 0.887215 | 0.289705 | 0.675704 | 0.35394 |
| \(u_{2}\) | -0.16324 | 0.461356 | 0.158162 | -0.02058 | 0.05631 |
表 2:原始变量与 Y 组典型变量之间的相关系数
| \(x_{1}\) | \(x_{2}\) | \(y_{1}\) | \(y_{2}\) | \(y_{3}\) | |
|---|---|---|---|---|---|
| \(v_{1}\) | 0.67872 | 0.610358 | 0.421115 | 0.982203 | 0.514487 |
| \(v_{2}\) | -0.0305 | 0.086212 | 0.846397 | -0.11014 | 0.301341 |
表 3:两组典型变量之间的典型相关系数
| 1 | 0.6879 |
| 2 | 0.1869 |
从这些表中,我们可以看到,两个表示外出活动特性的变量 \(x_1\) 和 \(x_2\) 与 \(u_1\) 的相关系数较大,说明 \(u_1\) 可以被视为形容外出活动特性的指标。在第一对典型变量中,\(v_1\) 与 \(y_2\) (代表家庭年收入)的相关系数较大,因此我们可以认为 \(v_1\) 主要代表了家庭的年收入。此外,\(u_1\) 和 \(v_1\) 之间的典型相关系数为 0.6879,说明这两个典型变量在一定程度上是相关的。
- 最后,对于原始变量的解释度,\(u_1\) 和 \(v_1\) 解释的本组原始变量的比率分别为 0.8803 和 0.4689。这表示 \(u_1\) 和 \(v_1\) 在一定程度上能够解释原始变量的变异。而且,\(\mathbf{X}\) 组的原始变量被 \(u_1\) 和 \(u_2\) 完全(100%)解释了,而 \(\mathbf{Y}\) 组的原始变量被 \(v_1\) 和 \(v_2\) 解释了 74.2%,说明典型变量确实能够在很大程度上表现出原始变量的特性。
3.程序
求解的MATLAB程序如下:
clc, clear;
% 加载数据
correlation_matrix = load('data104.txt');
% X组和Y组变量的数量
num_X = 2;
num_Y = 3;
num_min = min(num_X, num_Y);
% 提取X与X,Y与Y,Y与X的相关系数
correlation_XX = correlation_matrix([1:num_X], [1:num_X]);
correlation_YX = correlation_matrix([1:num_X], [num_X+1:end]);
correlation_XY = correlation_YX';
correlation_YY = correlation_matrix([num_X+1:end], [num_X+1:end]);
% 计算矩阵M1和M2
matrix_M1 = inv(correlation_XX) * correlation_YX * inv(correlation_YY) * correlation_XY;
matrix_M2 = inv(correlation_YY) * correlation_XY * inv(correlation_XX) * correlation_YX;
% 求M1的特征向量和特征值
[eigVec_M1, eigVal_M1] = eig(matrix_M1);
for i = 1:num_X
% 特征向量归一化,满足a's1a=1,特征向量乘±1,保证所有分量和为正
eigVec_M1(:, i) = eigVec_M1(:, i) / sqrt(eigVec_M1(:, i)' * correlation_XX * eigVec_M1(:, i));
eigVec_M1(:, i) = eigVec_M1(:, i) / sign(sum(eigVec_M1(:, i)));
end
% 计算特征值的平方根,按照从大到小排列
eigVal_M1 = sqrt(diag(eigVal_M1));
[eigVal_M1, ind1] = sort(eigVal_M1, 'descend');
% 取出X组的系数阵和典型相关系数
coef_X = eigVec_M1(:, ind1(1:num_min));
canCorrelation_X = eigVal_M1(1:num_min);
% 求M2的特征向量和特征值
[eigVec_M2, eigVal_M2] = eig(matrix_M2);
for i = 1:num_Y
% 特征向量归一化,满足b's2b=1,特征向量乘±1,保证所有分量和为正
eigVec_M2(:, i) = eigVec_M2(:, i) / sqrt(eigVec_M2(:, i)' * correlation_YY * eigVec_M2(:, i));
eigVec_M2(:, i) = eigVec_M2(:, i) / sign(sum(eigVec_M2(:, i)));
end
% 计算特征值的平方根,按照从大到小排列
eigVal_M2 = sqrt(diag(eigVal_M2));
[eigVal_M2, ind2] = sort(eigVal_M2, 'descend');
% 取出Y组的系数阵和典型相关系数
coef_Y = eigVec_M2(:, ind2(1:num_min));
canCorrelation_Y = eigVal_M2(1:num_min);
% 计算X,u;Y,v;X,v;Y,u的相关系数
correlation_XU = correlation_XX * coef_X;
correlation_YV = correlation_YY * coef_Y;
correlation_XV = correlation_YX * coef_Y;
correlation_YU = correlation_XY * coef_X;
% 计算X组、Y组原始变量被ui、vi解释的方差比例
ratio_XU = sum(correlation_XU.^2) / num_X;
ratio_XV = sum(correlation_XV.^2) / num_X;
ratio_YU = sum(correlation_YU.^2) / num_Y;
ratio_YV = sum(correlation_YV.^2) / num_Y;
% 输出结果
fprintf('X组的原始变量被u1~u%d解释的比例为%f\n', num_min, sum(ratio_XU));
fprintf('Y组的原始变量被v1~v%d解释的比例为%f\n', num_min, sum(ratio_YV));
习题10.5
1. 题目要求
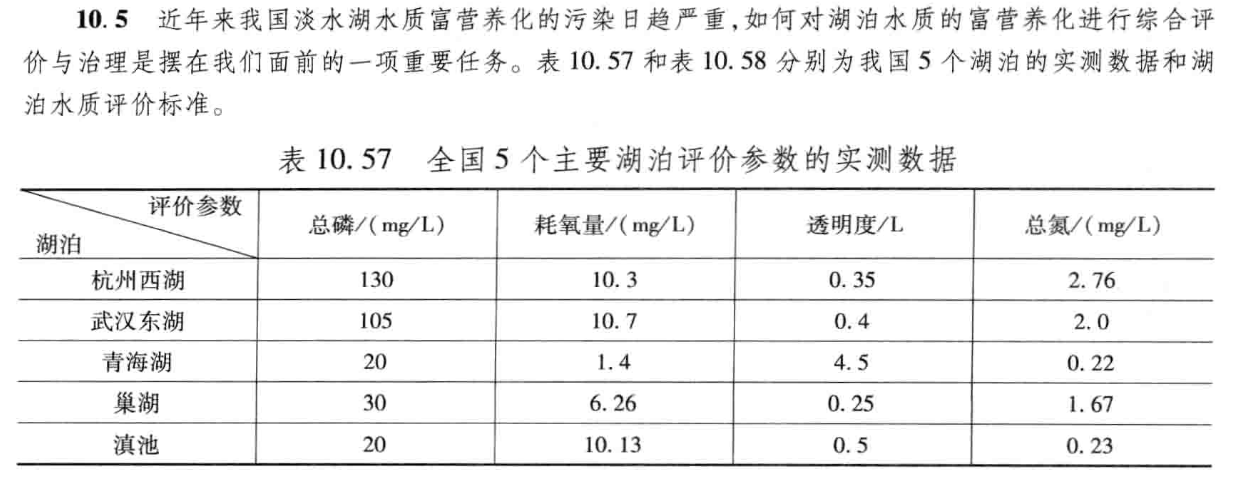
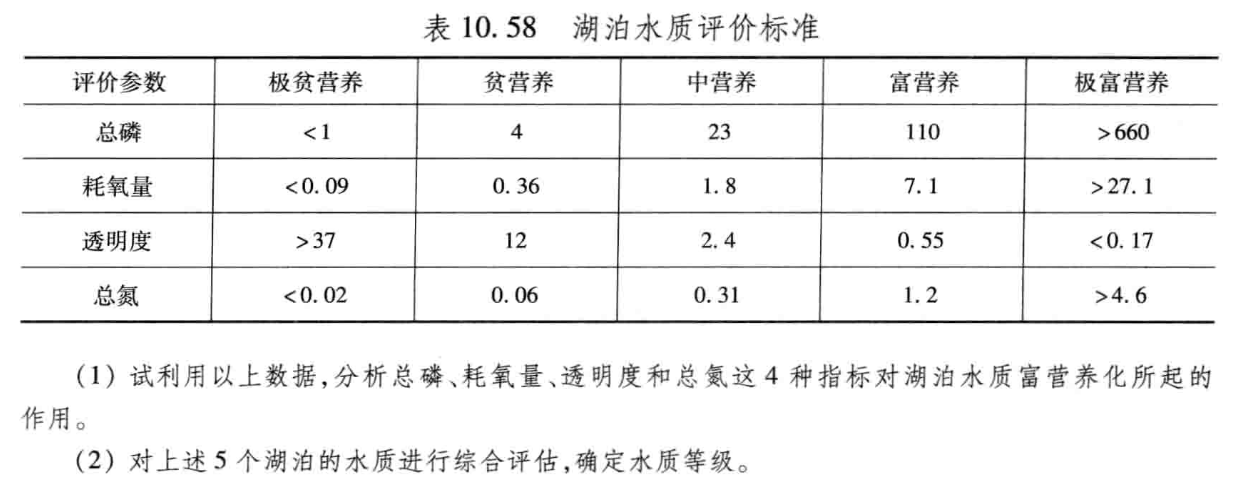
2.解题过程
解:
在进行综合评价之前,首先要对评价的指标进行分析。通常的评价指标分为效益型、成本型和固定型指标。效益型指标是指那些数值越大影响力越大的统计指标(也称为正向型指标);成本型指标是指数值越小越好的指标(亦称为逆向型指标);而固定型指标是指数值越接近某个常数越好的指标(又称为适度型指标)。如果各评价指标的属性不一致,则在进行综合评估时容易发生偏差,必须先对各评价指标统一属性。
- 建立无量纲化实测数据矩阵和评价标准矩阵。实测数据矩阵为 \(\mathbf{A}\) 和等级标准矩阵为 \(\mathbf{B}\),然后建立无量纲化实测数据矩阵 \(\mathbf{C}\) 和无量纲化等级标准矩阵 \(\mathbf{D}\)。其中,\(c_{ij}\) 和 \(d_{kt}\) 的计算方法如下:
\(c_{ij}\) 和 \(d_{kt}\) 的计算方式: $$ c_{ij} = \begin{cases} a_{ij} / \max_i a_{ij}, & \text{if } j \neq 3 \ \min_i a_{ij} / a_{ij}, & \text{if } j = 3 \end{cases} $$
$$ d_{kt} = \begin{cases} b_{kt} / \max_i b_{kt}, & \text{if } k \neq 3 \ \min_i b_{kt} / b_{kt}, & \text{if } k = 3 \end{cases} $$
- 计算 \(\mathbf{D}\) 的各行向量的均值 \(\mu_i\)、标准差 \(s_i\) 和变异系数 \(w_i\),以及权向量 \(\boldsymbol{w}\)。计算公式如下:
\(\mu_i\),\(s_i\) 和 \(w_i\) 的计算方式: $$ \mu_i = 0.2 \sum_{j=1}^{5} d_{ij} s_i = \sqrt{\frac{\sum_{j=1}^{5} (d_{ij}-\mu_i)^2}{4}} w_i = s_i / \mu_i $$
\(\boldsymbol{w}\) 的计算方式: $$ \boldsymbol{w} = [0.277,0.2447,0.2347,0.2442] $$
- 建立综合评价模型,计算 \(\mathbf{C}\) 中各个行向量到 \(\mathbf{D}\) 中各个列向量的欧氏距离 \(x_{ij}\) 和绝对值距离 \(y_{ij}\)。若 \(x_{ik}=\min_{1\leq j\leq5}{x_{ij}}\) 或 \(y_{ik}=\min_{1\leq j\leq5}{y_{ij}}\) 则表明第 \(i\) 个湖泊属于第 \(k\) 级。
然后,我们可以得到以下欧氏距离判别表和绝对值距离判别表。\(x_{ij}\) 和 \(y_{ij}\) 的计算方式: $$ x_{ij} = \sqrt{\sum_{k=1}^{4} (c_{ik}-d_{kj})^2}\ y_{ij} = \sum_{k=1}^{4} |c_{ik}-d_{kj}| $$
然后,我们可以得到以下欧氏距离判别表和绝对值距离判别表。
欧氏距离判别表
| 湖泊 | \(x_{i1}\) | \(x_{i2}\) | \(x_{i3}\) | \(x_{i4}\) | \(x_{i5}\) | 级别 |
|---|---|---|---|---|---|---|
| 杭州西湖 | 1.8472 | 1.8312 | 1.7374 | 1.3769 | 0.2881 | 5 |
| 武汉东湖 | 1.5959 | 1.5798 | 1.4859 | 1.1271 | 0.5034 | 5 |
| 青海湖 | 0.2185 | 0.2045 | 0.1367 | 0.3383 | 1.7917 | 3 |
| 巢湖 | 1.3201 | 1.3038 | 1.2082 | 0.8392 | 0.9591 | 4 |
| 滇池 | 1.0793 | 1.0650 | 0.9867 | 0.7328 | 1.3450 | 4 |
绝对值距离判别表
| 湖泊 | \(y_{i1}\) | \(y_{i2}\) | \(y_{i3}\) | \(y_{i4}\) | \(y_{i5}\) | 级别 |
|---|---|---|---|---|---|---|
| 杭州西湖 | 3.6631 | 3.6303 | 3.4374 | 2.6783 | 0.3231 | 5 |
| 武汉东湖 | 3.1436 | 3.1108 | 2.9178 | 2.1587 | 0.8427 | 5 |
| 青海湖 | 0.4062 | 0.3734 | 0.2110 | 0.5787 | 3.5800 | 3 |
| 巢湖 | 2.4071 | 2.3743 | 2.1814 | 1.4223 | 1.5791 | 4 |
| 滇池 | 1.6701 | 1.6374 | 1.4444 | 1.0660 | 2.3161 | 4 |
从上面的计算可知,尽管欧几里得距离与绝对值距离意义不同,但是对各湖泊水质的富营养化的评价等级是一样的,表明此处给出的方法具有稳定性。
3.程序
求解的MATLAB程序如下:
% 清除环境变量
clc; clear;
% 初始化实测数据矩阵
rawData = [130,10.3,0.35,2.76;
105,10.7,0.4,2.0;
20,1.4,4.5,0.22;
30,6.26,0.25,1.67;
20,10.13,0.5,0.23];
% 初始化等级标准矩阵
standardMatrix = [1,4,23,110,660;
0.09,0.36,1.8,7.1,27.1;
37,12.,2.4,0.55,0.17;
0.02,0.06,0.31,1.2,4.6];
% 进行无量纲化处理
normalizedRawData = rawData ./ repmat(max(rawData), size(rawData, 1), 1);
normalizedRawData(:, 3) = min(rawData(:, 3)) ./ rawData(:, 3);
normalizedStandardMatrix = standardMatrix ./ repmat(max(standardMatrix, [], 2), 1, size(standardMatrix, 2));
normalizedStandardMatrix(3, :) = min(standardMatrix(3, :)) ./ standardMatrix(3, :);
% 计算均值和标准差
average = mean(standardMatrix, 2);
standardDeviation = std(standardMatrix, [], 2);
% 计算权重
weights = standardDeviation ./ average;
weights = weights / sum(weights);
% 计算欧式距离
euclideanDistances = dist(normalizedRawData, normalizedStandardMatrix);
% 计算绝对值距离
absoluteDistances = mandist(normalizedRawData, normalizedStandardMatrix);
习题10.6(1)
1. 题目要求
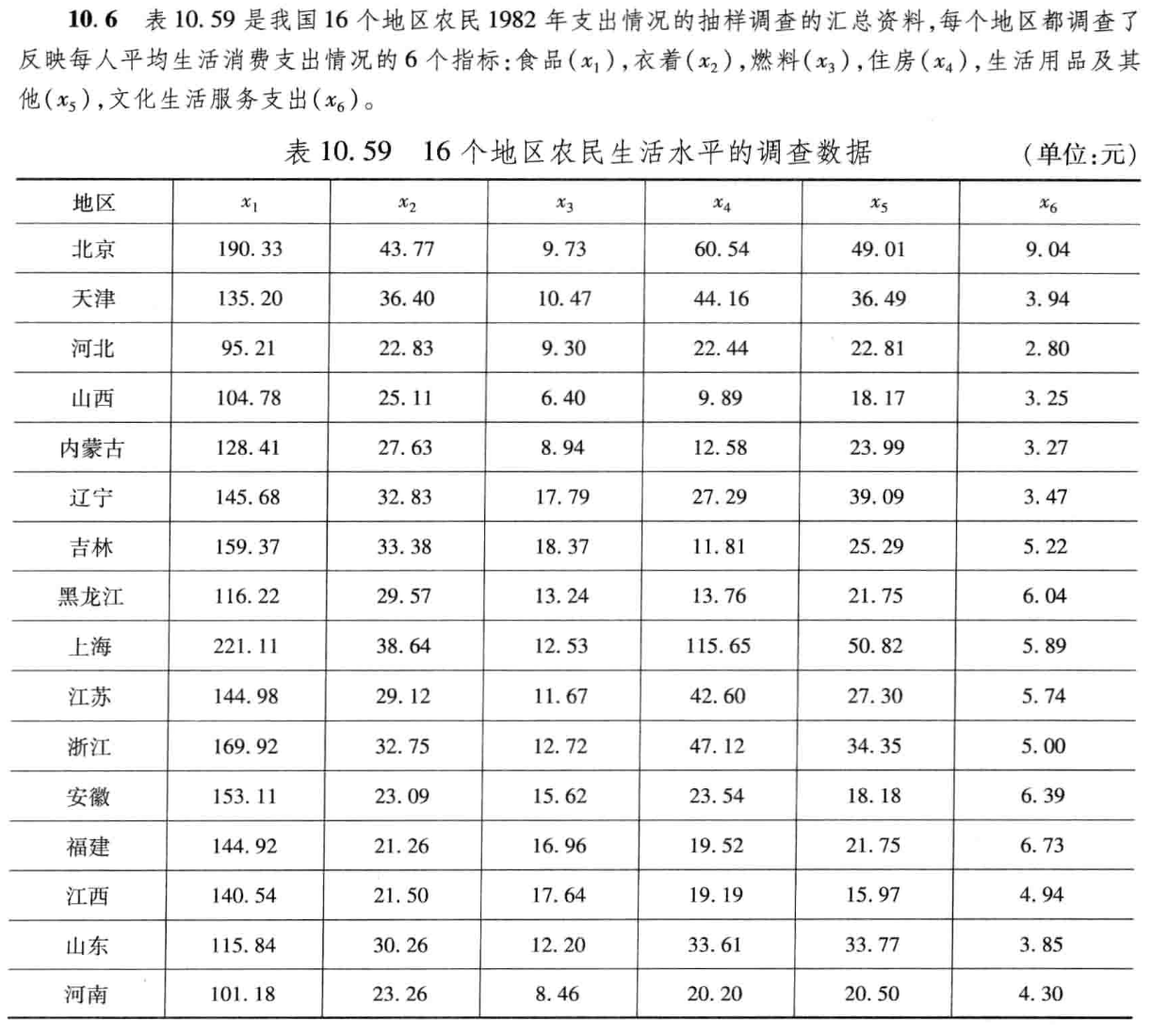
2.解题过程——对应分析
解:
分别用 \(i=1,\dots,16\) 表示,以 \(a_{ij}\) 表示第 i 个地区第 j 个指标变量 \(x_j\) 的取值。
记: $$ \mathbf{A}=(a_{ij}){16\times6} $$ 记: $$ a{i\cdot}=\sum_{j=1}^{6}a_{ij},a_{\cdot j}=\sum_{i=1}^{16}a_{ij} $$ 首先把 \(\mathbf{A}\) 化为规格化的“概率”矩阵 \(\mathbf{P}\) , 记 \(\mathbf{P}=(p_{ij})_{16\times6}\) ,其中 \(p_{ij}=a_{ij}/\mathbf{T}\) ,\(\mathbf{T}=\sum_{i=1}^{16}\sum_{j=1}^{6}a_{ij}\)。再对数据进行对应变换,令 \(\mathbf{B}=(b_{ij})_{16\times6}\) ,其中: $$ b_{ij}=\frac{p_{ij}-p_{i\cdot}p_{\cdot j}}{\sqrt{p_{i\cdot}p_{\cdot j}}}
= \frac{a_{ij}-a_{i\cdot}a_{\cdot j}/\mathbf{T}}{\sqrt{a_{i\cdot}a_{\cdot j}}},
i=1,2,\dots, 16,j=1,2,\dots,6. $$ 对 \(\mathbf{B}\) 进行奇异值分解,\(\mathbf{B}=\mathbf{U}\varLambda \mathbf{V}^{\mathbf{T}} (,其中 \(\mathbf{U}\) 为 \(16\times 16\) 正交矩阵,\)\mathbf{V}\)为 \(6\times6\) 正交矩阵,\(\varLambda =\begin{bmatrix} \varLambda_m &0\\ 0&0 \end{bmatrix}\),这里 $ \varLambda_m=diag(d_1,\dots,d_m) $ ,其中 \(d_i(i=1,2,\dots,m)\) 为 \(\mathbf{B}\) 的奇异值。
记 \(\mathbf{U}=[\mathbf{U_1} \vdots \mathbf{U_2}],\mathbf{V}=[\mathbf{V_1} \vdots \mathbf{V_2}]\) ,其中 \(\mathbf{U_1}\) 为\(16\times m\) 的列正交矩阵,\(\mathbf{V_1}\) 为 \(6\times m\) 的列正交矩阵,则 \(\mathbf{B}\) 的奇异值分解式等价于\(\mathbf{B}=\mathbf{U_1}\varLambda\mathbf{V_1}^T\)。
记 \(\mathbf{D_r}=diag(p_{1\cdot},p_{2\cdot},\dots,p_{16\cdot}),\mathbf{D_c}=diag(p_{\cdot1},p_{\cdot2},\dots,p_{\cdot6})\) ,其中 \(p_{i\cdot}=\sum_{j=1}^{6}p_{ij}\) ,\(p_{\cdot j}=\sum_{i=1}^{16}p_{ij}\)。则列轮廓的坐标为 \(\mathbf{F}=\mathbf{D}_{c}^{-1/2}\mathbf{V_1}\varLambda_m\) ,行轮廓的坐标为 \(\mathbf{G}=\mathbf{D}_{r}^{-1/2}\mathbf{V_1}\varLambda_m\) 。最后通过贡献率的比较确定需要截取的维数,形成对应分析图。
计算 \(\mathbf{B^T}\mathbf{B}\) 的特征值,惯量,表示相应维数对各类别的解释量,最大维数 \(m=\min{16-1,6-1}\) ,本例最多可以产生5个维数。从下表可看出,第一维数的解释量达 77.4% ,前两个维数的解释度已达92.1%。
| 维数 | 奇异值 | 惯量 | 贡献率 | 累积贡献率 |
|---|---|---|---|---|
| 1 | 0.189893 | 0.036059 | 0.773764 | 0.773764 |
| 2 | 0.082831 | 0.006861 | 0.147224 | 0.920988 |
| 3 | 0.047138 | 0.002222 | 0.047618 | 0.968669 |
| 4 | 0.03113 | 0.000969 | 0.020795 | 0.989464 |
| 5 | 0.022159 | 0.000491 | 0.010536 | 1 |
行坐标
| 北京 | 天津 | 河北 | 山西 | 内蒙古 | 辽宁 | |
|---|---|---|---|---|---|---|
| 第一维 | -0.07905 | -0.06783 | -0.26354 | 0.457766 | 0.07715 | -0.13567 |
| 第二维 | -0.0354 | 0.138818 | -0.10045 | -0.05715 | 0.156316 | -0.08455 |
| 吉林 | 黑龙江 | 上海 | 江苏 | 浙江 | 安徽 | |
|---|---|---|---|---|---|---|
| 第一维 | -0.27126 | -0.19757 | 0.386809 | 0.086955 | 0.079122 | -0.14212 |
| 第二维 | -0.00074 | 0.045985 | -0.07833 | -0.04222 | -0.01969 | -0.14225 |
| 福建 | 江西 | 山东 | 河南 | |
|---|---|---|---|---|
| 第一维 | -0.17469 | -0.18859 | 0.069823 | -0.1462 |
| 第二维 | -0.11317 | -0.1527 | 0.100318 | 0.032858 |
列坐标
| x1 | x2 | x3 | x4 | x5 | x6 | |
|---|---|---|---|---|---|---|
| 第一维 | -0.07905 | -0.06783 | -0.26354 | 0.457766 | 0.07715 | -0.13567 |
| 第二维 | -0.0354 | 0.138818 | -0.10045 | -0.05715 | 0.156316 | -0.08455 |
在下图中,给出16个地区和6个指标在相同坐标系上绘制的散布图。
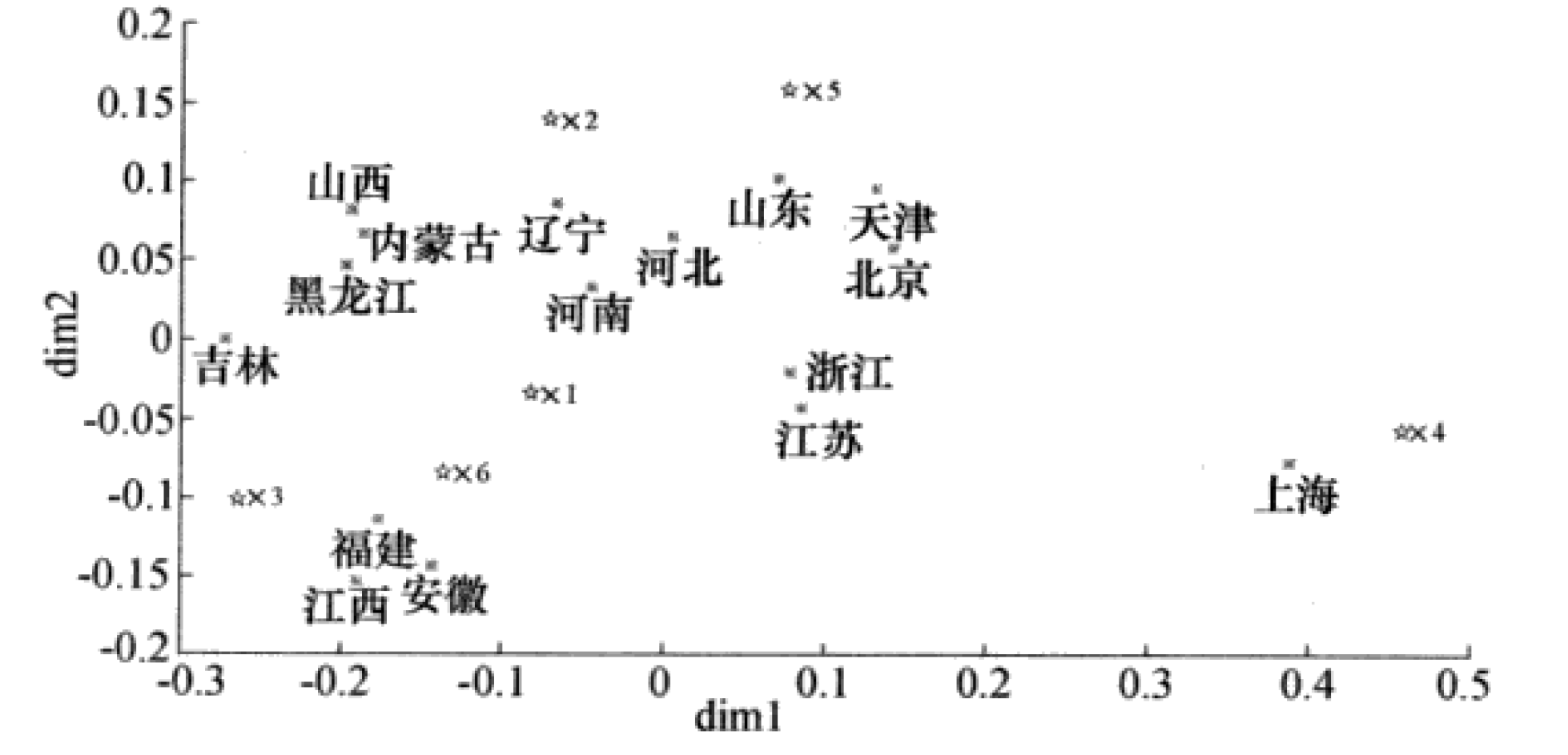
从图中可以看出,地区和指标点可以分为两类,
第一类包括指标点 \(x_4,x_5\) ,地区点为北京、天津、河北、上海、江苏、浙江、山东;
第二类包括指标点 \(x_1,x_2,x_3,x_6\) ,地区点为其余地区。
3.程序
求解的MATLAB程序如下:
clc, clear
% 原始数据,其中包含了16个地区的6项指标
originalData = [190.33, 43.77, 9.73, 60.54, 49.01, 9.04; ...
135.20, 36.40, 10.47, 44.16, 36.49, 3.94; ...
95.21, 22.83, 9.30, 22.44, 22.81, 2.80; ...
104.78, 25.11, 6.40, 9.89, 18.17, 3.25; ...
128.41, 27.63, 8.94, 12.58, 23.99, 3.27; ...
145.68, 32.83, 17.79, 27.29, 39.09, 3.47; ...
159.37, 33.38, 18.37, 11.81, 25.29, 5.22; ...
116.22, 29.57, 13.24, 13.76, 21.75, 6.04; ...
221.11, 38.64, 12.53, 115.65, 50.82, 5.89; ...
144.98, 29.12, 11.67, 42.60, 27.30, 5.74; ...
169.92, 32.75, 12.72, 47.12, 34.35, 5.00; ...
153.11, 23.09, 15.62, 23.54, 18.18, 6.39; ...
144.92, 21.26, 16.96, 19.52, 21.75, 6.73; ...
140.54, 21.50, 17.64, 19.19, 15.97, 4.94; ...
115.84, 30.26, 12.20, 33.61, 33.77, 3.85; ...
101.18, 23.26, 8.46, 20.20, 20.50, 4.30];
% 计算原始数据的总和
totalSum = sum(sum(originalData));
% 计算原始数据的比例
ratioData = originalData / totalSum;
% 计算行和列的比例
rowRatio = sum(ratioData, 2);
columnRatio = sum(ratioData);
% 计算行剖面数据
Row_prifile = originalData ./ repmat(sum(originalData, 2), 1, size(originalData, 2));
% 计算B(B为对应分析的基础矩阵)
B = (ratioData - rowRatio * columnRatio) ./ sqrt(rowRatio*columnRatio);
% 对B矩阵进行奇异值分解,得到U,S,V矩阵
[U, S, V] = svd(B, 'econ');
% 对V矩阵列求和并根据其符号调整权重
W1 = sign(repmat(sum(V), size(V, 1), 1));
% 对U矩阵列求和并根据其符号调整权重
W2 = sign(repmat(sum(V), size(U, 1), 1));
% 应用权重调整V和U矩阵
V_adjusted = V .* W1;
U_adjusted = U .* W2;
% 计算lambda(特征值的平方)
lambda = diag(S).^2;
% 计算卡方统计量
chi2Square = totalSum * (lambda);
% 计算总的卡方统计量
totalChi2Square = sum(chi2Square);
% 计算贡献率
contributionRate = lambda / sum(lambda);
% 计算累计贡献率
cumulativeRate = cumsum(contributionRate);
% 计算行轮廓坐标
beta = diag(rowRatio.^(-1 / 2)) * U_adjusted;
G = beta * S
% 计算列轮廓坐标
alpha = diag(columnRatio.^(-1 / 2)) * V_adjusted;
F = alpha * S
% 计算样本点的个数
numOfSample = size(G, 1);
% 计算坐标的取值范围
range = minmax(G(:, [1, 2])');
% 画图略
4.结果
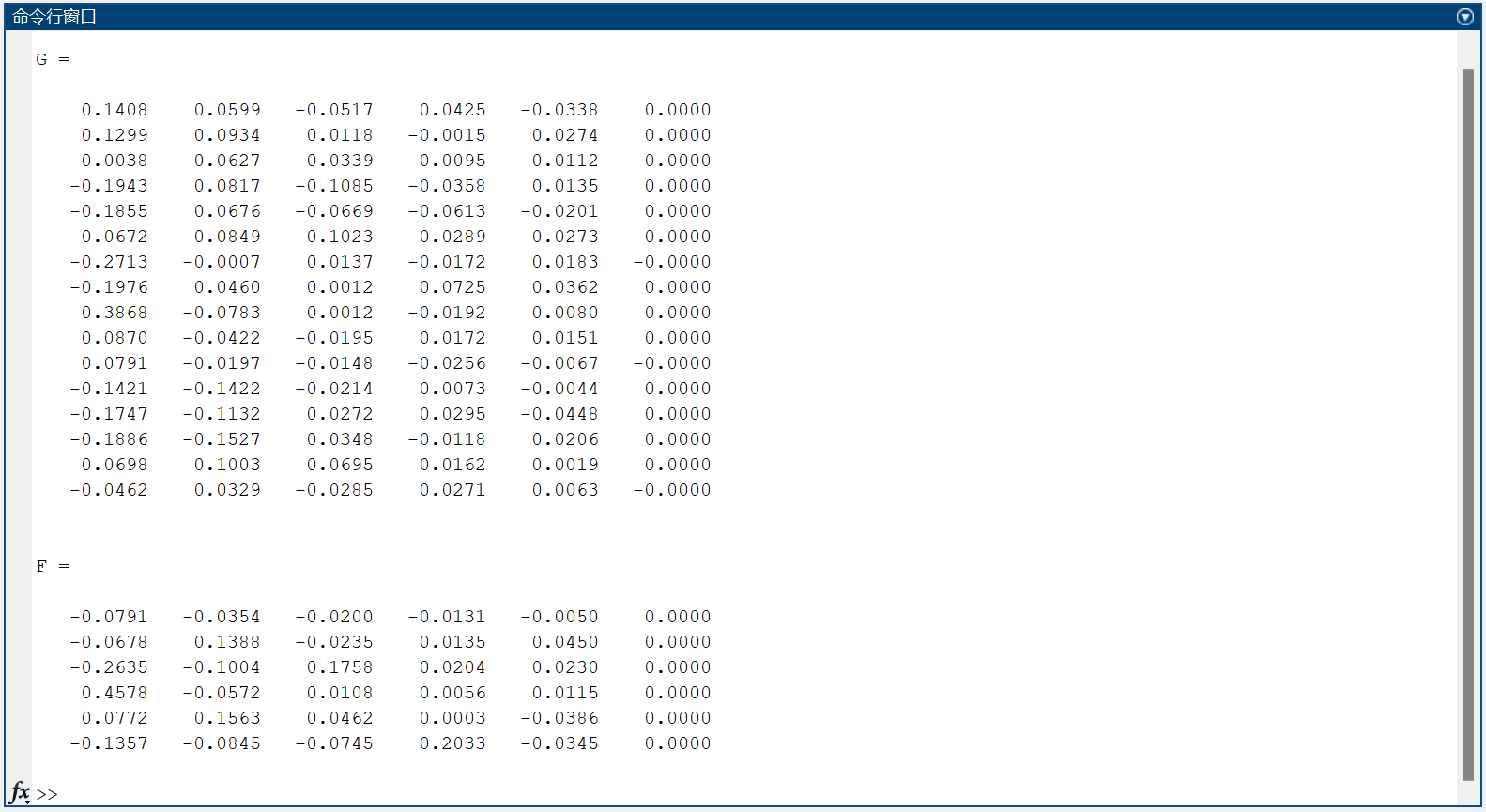
详见上文分析过程,地区和指标点可以分为两类,
第一类包括指标点 \(x_4,x_5\) ,地区点为北京、天津、河北、上海、江苏、浙江、山东;
第二类包括指标点 \(x_1,x_2,x_3,x_6\) ,地区点为其余地区。
习题10.6(2)
1. 题目要求
同上。
2.解题过程——R型因子分析
解:
对数据进行标准化处理。
计算变量间的相关系数得出相关矩阵 \(\mathbf{R}\) ,然后计算初等载荷矩阵 \(\mathbf{\Lambda_1}\) 。
计算得到特征根与各因子的贡献如下表所示。
| value | x1 | x2 | x3 | x4 | x5 | x6 |
|---|---|---|---|---|---|---|
| 特征值 | 3.55842 | 1.316252 | 0.608239 | 0.373383 | 0.107178 | 0.036527 |
| 贡献率 | 59.30701 | 21.93754 | 10.13732 | 6.223052 | 1.786295 | 0.608786 |
| 累积贡献率 | 59.30701 | 81.24454 | 91.38187 | 97.60492 | 99.39121 | 100 |
选择 \(m(m\leq6)\) 个主因子,构造因子模型: $$ \begin{align} \begin{cases} \widetilde{x}1=\alpha{11}\widetilde{F}1+\alpha{12}\widetilde{F}2+\alpha{13}\widetilde{F}3 \ \vdots\ \widetilde{x}_7=\alpha{71}\widetilde{F}1+\alpha{72}\widetilde{F}2+\alpha{73}\widetilde{F}_3 \end{cases}\end{align} $$ 求得因子载荷等估计。
最终,通过表格,可以看出,得到了3个因子,第一个因子是穿住用因子,第二个因子是燃料因子,第3个因子是文化因子。
第(1)问中得到 \(x_4,x_5\) 是一类变量,这里得到 \(x_2,x_4,x_5\) 是一类变量,略有差异。
3.程序
求解的MATLAB程序如下:
clc, clear
% 原始数据,包含了16个地区的6项指标
originalData = [190.33, 43.77, 9.73, 60.54, 49.01, 9.04; ...
135.20, 36.40, 10.47, 44.16, 36.49, 3.94; ...
95.21, 22.83, 9.30, 22.44, 22.81, 2.80; ...
104.78, 25.11, 6.40, 9.89, 18.17, 3.25; ...
128.41, 27.63, 8.94, 12.58, 23.99, 3.27; ...
145.68, 32.83, 17.79, 27.29, 39.09, 3.47; ...
159.37, 33.38, 18.37, 11.81, 25.29, 5.22; ...
116.22, 29.57, 13.24, 13.76, 21.75, 6.04; ...
221.11, 38.64, 12.53, 115.65, 50.82, 5.89; ...
144.98, 29.12, 11.67, 42.60, 27.30, 5.74; ...
169.92, 32.75, 12.72, 47.12, 34.35, 5.00; ...
153.11, 23.09, 15.62, 23.54, 18.18, 6.39; ...
144.92, 21.26, 16.96, 19.52, 21.75, 6.73; ...
140.54, 21.50, 17.64, 19.19, 15.97, 4.94; ...
115.84, 30.26, 12.20, 33.61, 33.77, 3.85; ...
101.18, 23.26, 8.46, 20.20, 20.50, 4.30];
% 数据标准化
standardizedData = zscore(originalData);
% 计算相关性矩阵
correlationMatrix = corrcoef(standardizedData);
% 使用主成分分析方法对相关性矩阵进行处理,得到特征向量、特征值和贡献率
[eigenvectors, eigenvalues, contribution] = pcacov(correlationMatrix);
% 计算累积贡献率
cumulativeContribution = cumsum(contribution);
% 根据特征向量的符号进行调整
adjustedSigns = repmat(sign(sum(eigenvectors)), size(eigenvectors, 1), 1);
adjustedEigenvectors = eigenvectors .* adjustedSigns;
% 根据特征值进行缩放
scaledFactors = repmat(sqrt(eigenvalues)', size(adjustedEigenvectors, 1), 1);
scaledEigenvectors = adjustedEigenvectors .* scaledFactors;
% 计算贡献率
contribution1 = sum(scaledEigenvectors.^2);
% 选择的因子数量
factorNum = 3;
% 根据选择的因子数量得到对应的因子
selectedFactors = scaledEigenvectors(:, [1:factorNum]);
% 使用方差最大法进行因子旋转
[rotatedFactors, factorMatrix] = rotatefactors(selectedFactors, 'method', 'varimax')
% 合并旋转后的因子和其他因子
mergedFactors = [rotatedFactors, scaledEigenvectors(:, [factorNum + 1:end])];
% 计算因子载荷量
factorLoads = sum(rotatedFactors.^2, 2)
% 计算贡献率
contribution2 = sum(mergedFactors.^2)
% 计算每个因子的贡献率
contributionRate = contribution2(1:factorNum) / sum(contribution2);
% 计算因子得分系数矩阵
factorScoreCoefficients = inv(correlationMatrix) * rotatedFactors;
4.结果
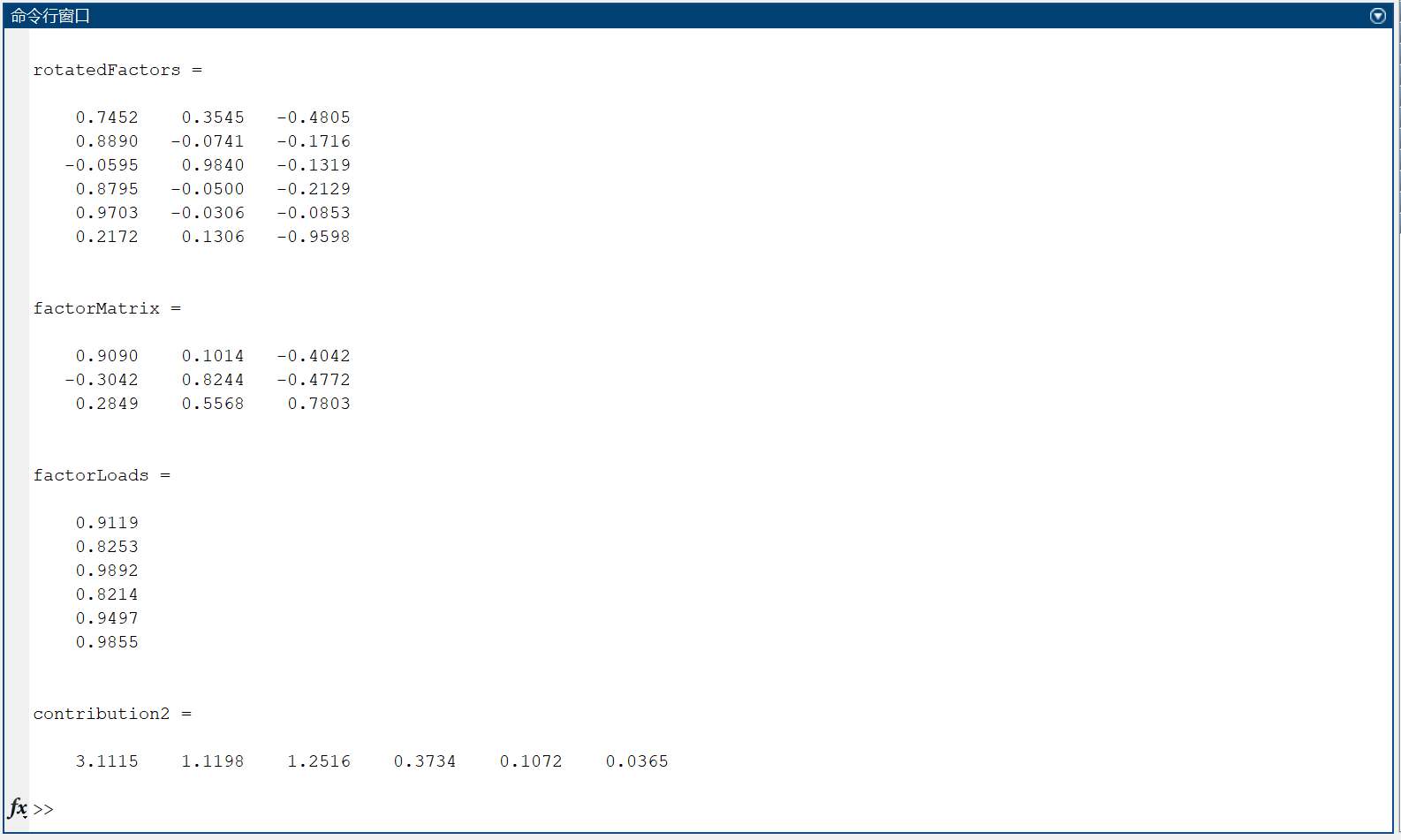
求得因子载荷等估计如下表所示。
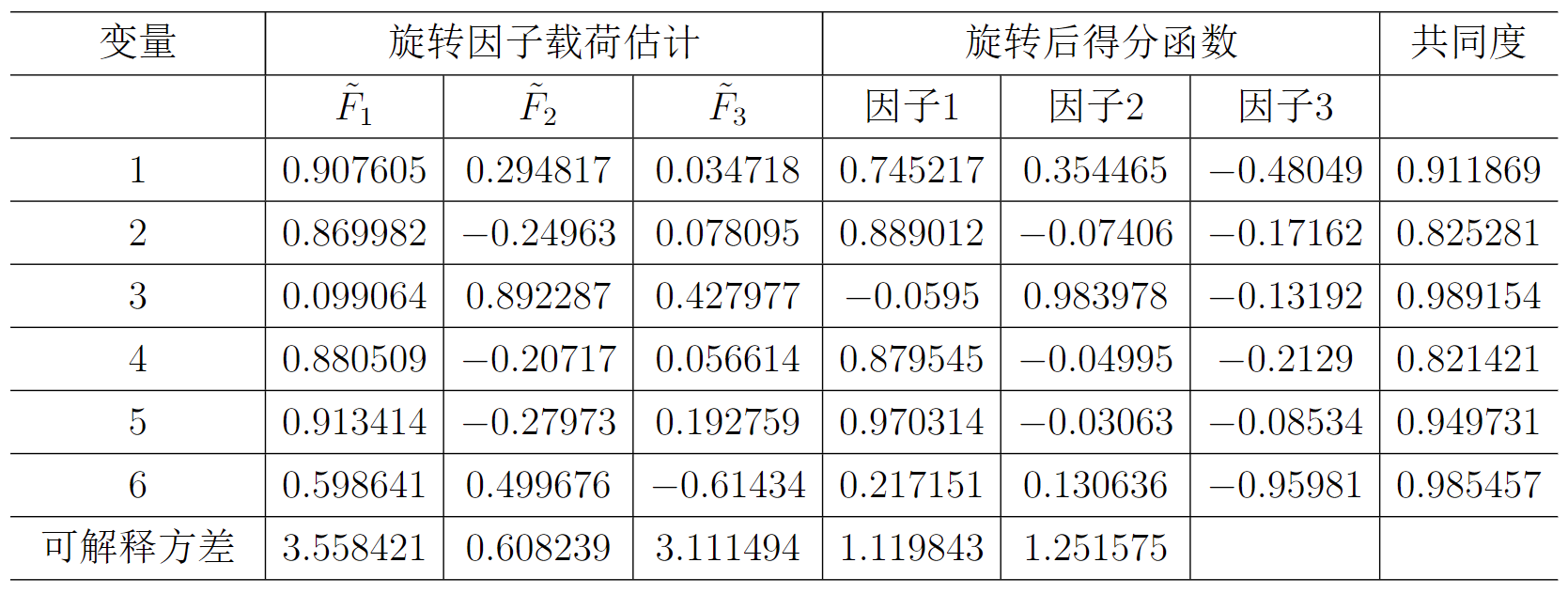
可以看出,得到了3个因子,第一个因子是穿住用因子,第二个因子是燃料因子,第3个因子是文化因子。
第(1)问中得到 \(x_4,x_5\) 是一类变量,这里得到 \(x_2,x_4,x_5\) 是一类变量,略有差异。
习题10.6(3)
1. 题目要求
同上。
2.解题过程——聚类分析
解:
首先计算变量间的相关系数。用两变量\(x_j\)与\(x_k\)的相关系数作为它们的相似性度量,即\(x_j\)与\(x_k\)的相似系数为 $$ r_{jk} = \frac{\sum_{i=1}^{16}(a_{ij}-\mu_{j})(a_{ik}-\mu_k)}
{[\sum_{i=1}^{16}(a_{ij}-\mu_{j})^2\sum_{i=1}^{16}(a_{ik}-\mu_k)^2]^{1/2}},j,k=1,\dots,6. $$ 然后计算6个变量两两之间的距离,构造距离矩阵。
接着使用最短距离法来测量类与类之间的距离,记类\(G_{p}\)和\(G_{q}\)之间的距离: $$ D(G_p,G_q) = \min_{i\in G_p,k\in G_q }{d_{ik}}. $$ 变量聚类的结果是变量\(x_3\)自成一类,其他变量为一类。画出的变量聚类图如下图所示。
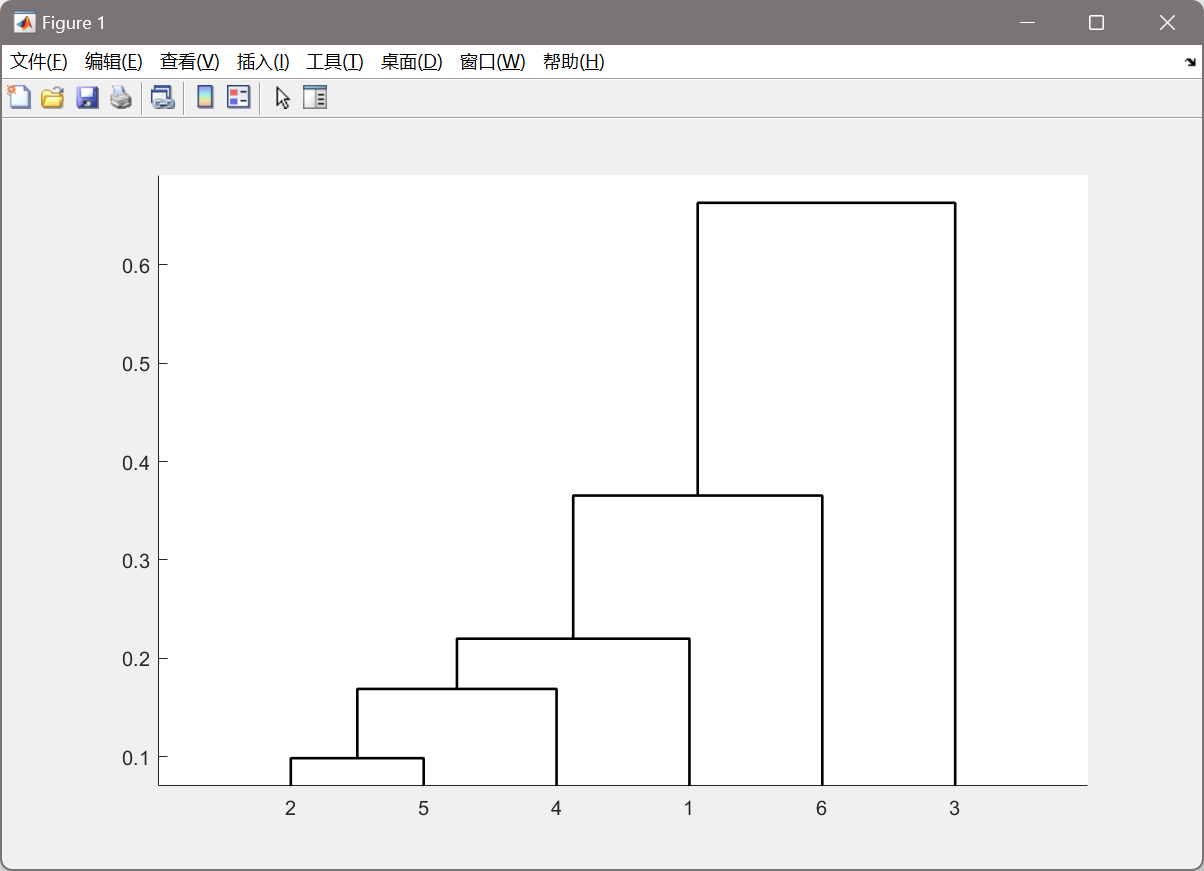
最后进行样本点聚类的\(\mathbf{Q}\)型聚类分析。
计算16个样本点之间的两两马氏距离。
类与类间相似性度量。
画聚类图,并对样本点进行分类。
样本点的聚类结果如下图所示。通过聚类图,可以把地区分成4类,北京自成一类,吉林自成一类,上海自成一类,其他地区为一类。
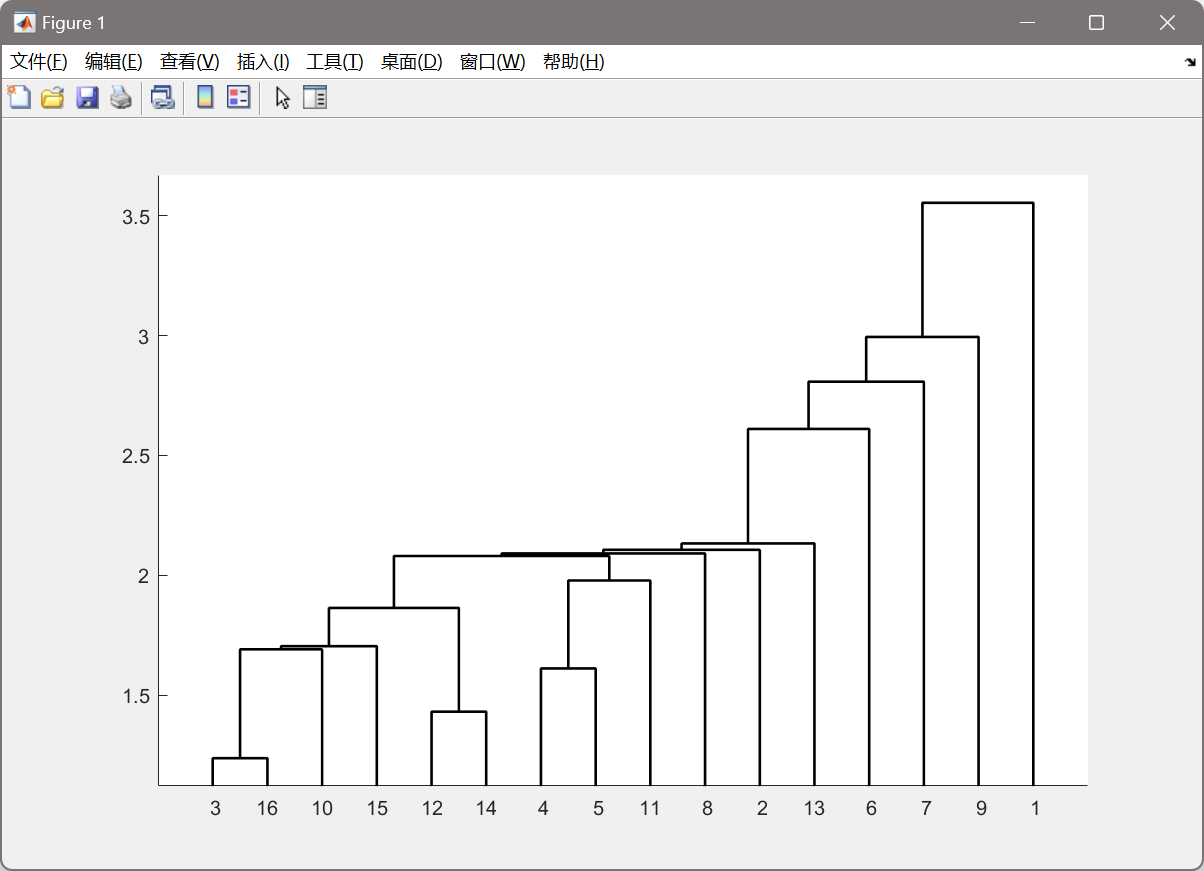
3.程序
求解的MATLAB程序如下:R型聚类
clc, clear
% 原始数据,包含了16个地区的6项指标
originalData = [190.33, 43.77, 9.73, 60.54, 49.01, 9.04; ...
135.20, 36.40, 10.47, 44.16, 36.49, 3.94; ...
95.21, 22.83, 9.30, 22.44, 22.81, 2.80; ...
104.78, 25.11, 6.40, 9.89, 18.17, 3.25; ...
128.41, 27.63, 8.94, 12.58, 23.99, 3.27; ...
145.68, 32.83, 17.79, 27.29, 39.09, 3.47; ...
159.37, 33.38, 18.37, 11.81, 25.29, 5.22; ...
116.22, 29.57, 13.24, 13.76, 21.75, 6.04; ...
221.11, 38.64, 12.53, 115.65, 50.82, 5.89; ...
144.98, 29.12, 11.67, 42.60, 27.30, 5.74; ...
169.92, 32.75, 12.72, 47.12, 34.35, 5.00; ...
153.11, 23.09, 15.62, 23.54, 18.18, 6.39; ...
144.92, 21.26, 16.96, 19.52, 21.75, 6.73; ...
140.54, 21.50, 17.64, 19.19, 15.97, 4.94; ...
115.84, 30.26, 12.20, 33.61, 33.77, 3.85; ...
101.18, 23.26, 8.46, 20.20, 20.50, 4.30];
% 计算相关性矩阵
correlationMatrix = corrcoef(originalData);
% 计算距离矩阵
distanceMatrix = 1 - abs(correlationMatrix);
distanceMatrix = tril(distanceMatrix);
% 将距离矩阵转为一维向量
distanceVector = nonzeros(distanceMatrix);
distanceVector = distanceVector';
% 使用层次聚类算法进行聚类
linkageCluster = linkage(distanceVector);
% 选择最大聚类数量为2,得到每个样本的类别
clusterLabels = cluster(linkageCluster, 'maxclust', 2);
% 找到属于第一类的样本
index1 = find(clusterLabels == 1);
index1 = index1'
% 找到属于第二类的样本
index2 = find(clusterLabels == 2);
index2 = index2'
% 生成树状图
h = dendrogram(linkageCluster);
% 设置树状图的颜色和线条宽度
set(h, 'Color', 'k', 'LineWidth', 1.3)
求解的MATLAB程序如下:Q型聚类
clc, clear
% 原始数据,包含了16个地区的6项指标
originalData = [190.33, 43.77, 9.73, 60.54, 49.01, 9.04; ...
135.20, 36.40, 10.47, 44.16, 36.49, 3.94; ...
95.21, 22.83, 9.30, 22.44, 22.81, 2.80; ...
104.78, 25.11, 6.40, 9.89, 18.17, 3.25; ...
128.41, 27.63, 8.94, 12.58, 23.99, 3.27; ...
145.68, 32.83, 17.79, 27.29, 39.09, 3.47; ...
159.37, 33.38, 18.37, 11.81, 25.29, 5.22; ...
116.22, 29.57, 13.24, 13.76, 21.75, 6.04; ...
221.11, 38.64, 12.53, 115.65, 50.82, 5.89; ...
144.98, 29.12, 11.67, 42.60, 27.30, 5.74; ...
169.92, 32.75, 12.72, 47.12, 34.35, 5.00; ...
153.11, 23.09, 15.62, 23.54, 18.18, 6.39; ...
144.92, 21.26, 16.96, 19.52, 21.75, 6.73; ...
140.54, 21.50, 17.64, 19.19, 15.97, 4.94; ...
115.84, 30.26, 12.20, 33.61, 33.77, 3.85; ...
101.18, 23.26, 8.46, 20.20, 20.50, 4.30];
% 计算原始数据的协方差
covarianceMatrix = cov(originalData);
% 初始化距离矩阵
distanceMatrix = zeros(size(originalData, 1));
% 计算Q型距离
for j = 1:15
for i = j+1:16
distanceMatrix(i,j) = sqrt((originalData(i,:) - originalData(j,:)) * inv(covarianceMatrix) * (originalData(i,:) - originalData(j,:))');
end
end
% 将距离矩阵转为一维向量
distanceVector = nonzeros(distanceMatrix);
distanceVector = distanceVector';
% 使用层次聚类算法进行聚类
linkageCluster = linkage(distanceVector);
% 生成树状图
dendro = dendrogram(linkageCluster);
% 设置树状图的颜色和线条宽度
set(dendro,'Color','k','LineWidth',1.3)
4.结果

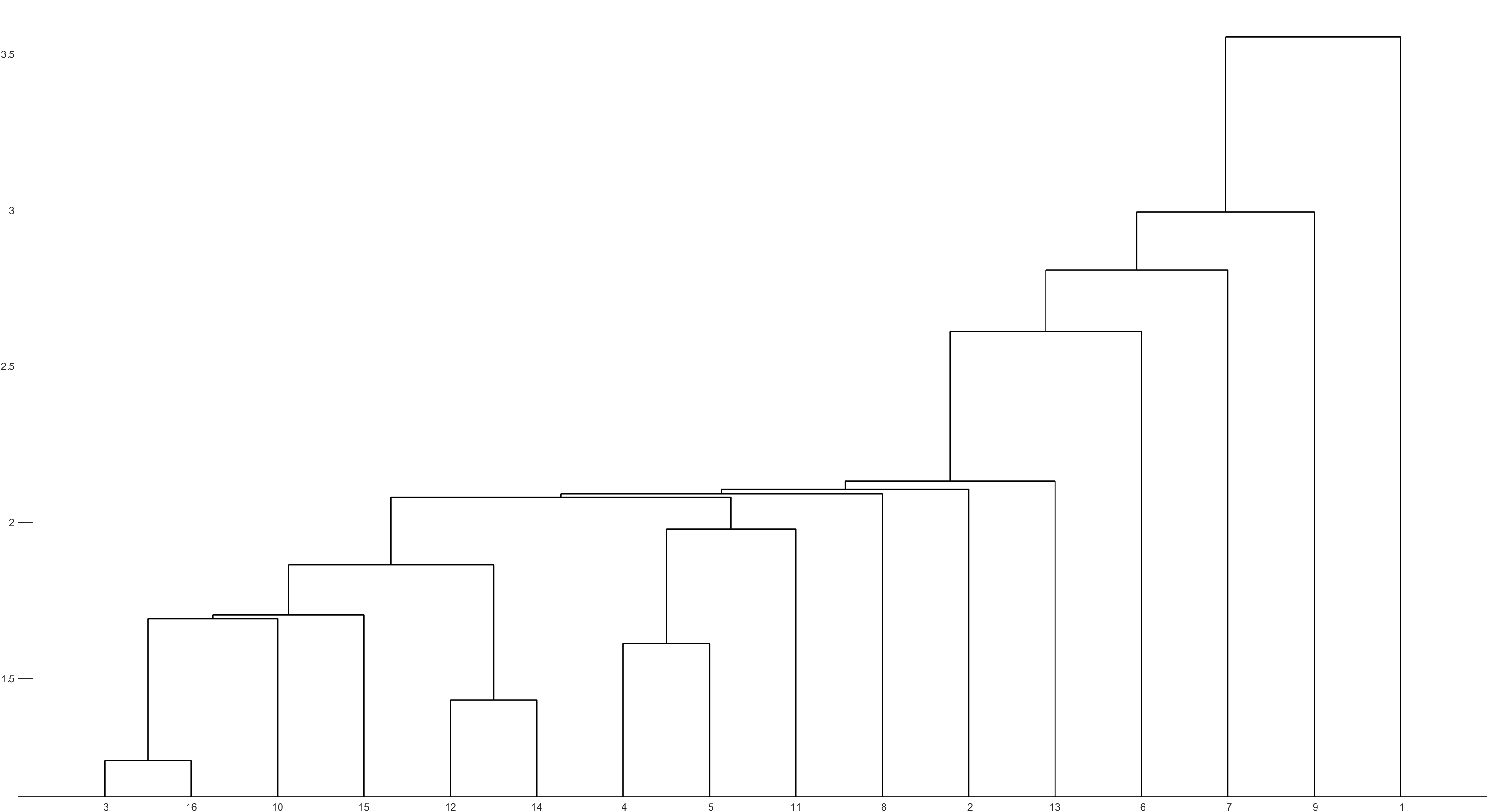
变量\(x_3\)自成一类,其他变量为一类。
北京自成一类,吉林自成一类,上海自成一类,其他地区为一类。