第十一讲-因子分析(聚类与主成分)
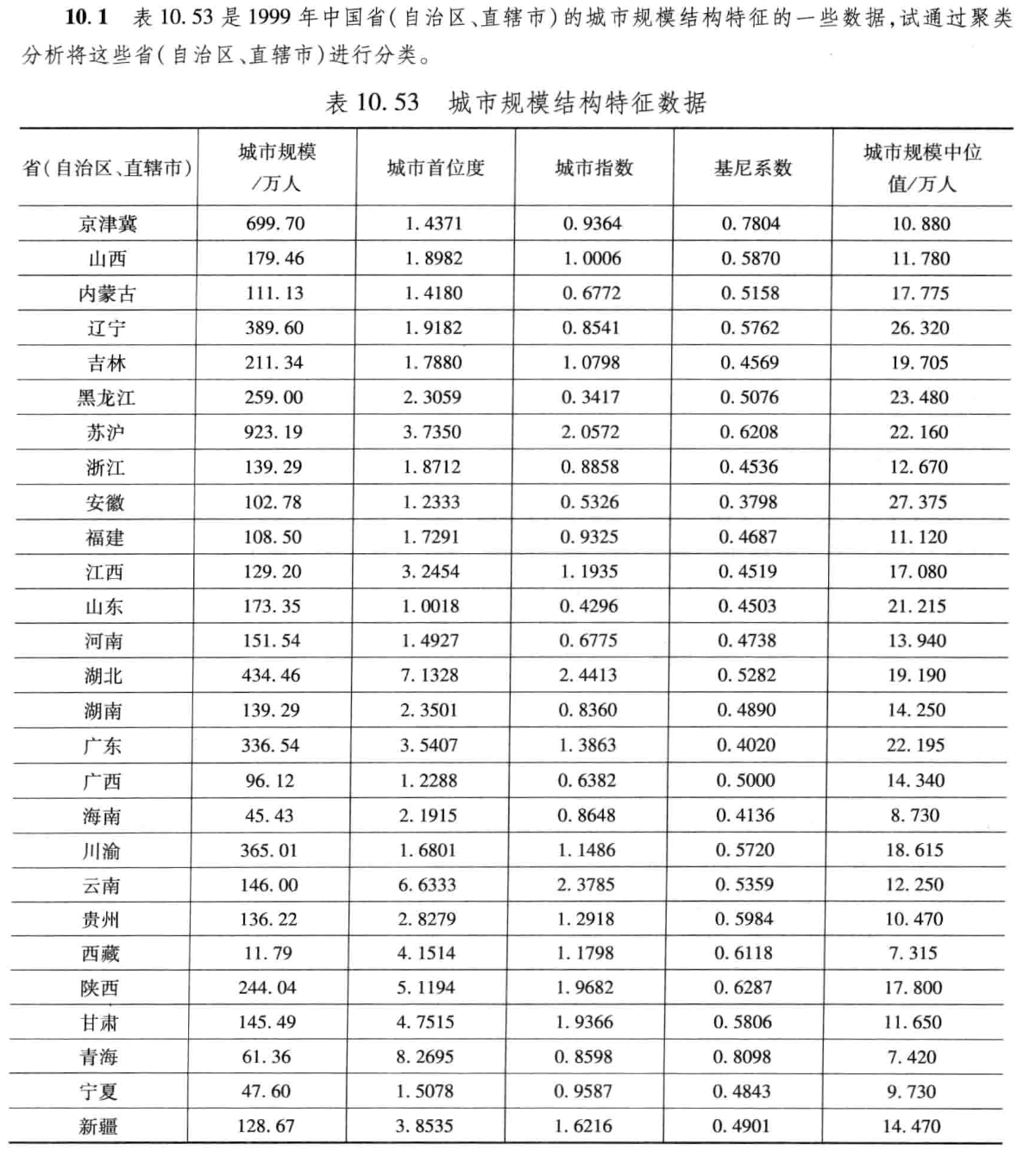
习题10.1
1. 题目要求
2.解题过程
解:
用 \(i=1,2...,27\) 表示京津冀、山西、\(...\)、新疆27个省、自治区, \(x_j(j=1,...,5)\) 分别表示指标变量城市规模城市首位度、城市指数、基尼系数、城市规模中位值。
(1)数据标准化
用 \(a_{ij}\) 表示第i个省第j个指标变量的取值。
首先将各指标值 \(a_{ij}\) 转化为标准化指标值: $$ b_{ij}\,=\,{\frac{a_{ij}-\mu_{{i}}}{s_{j}}}\,;i\,=\,1\,,2\,,\cdots,27\,;j\,=\,1\,,\cdots,5. $$ 其中,\(\mu_{j}\) 是第j个指标的样本均值,\(s_j\) 是第j个指标的样本标准差: $$ \mu_{j}\,=\,{\frac{1}{27}}\sum_{i=1}^{27}a_{ij} $$
(2)计算27个样本点彼此之间的距离,构造距离矩阵: $$ d_{i k}~=~{\sqrt{\sum_{j=1}^{5}\,\left(\,b_{i j}\,-\,b_{k j}\right)^{2}}} $$ 使用最短距离法来测量类与类之间的距离: $$ D(G_{p},G_{q})\;=\;\operatorname*{min}{i\in G_p,k\in G_q}\left|d{ik}\right| $$ (3)
构造27个类,每一个类中只包含一个样本点,每一类的平台高度均为零。
(4)
合并距离最近的两类为新类,并且以这两类间的距离值作为聚类图中的平台高度。
(5)
若类的个数等于1,转人步骤(6),否则,计算新类与当前各类的距离,回到步骤(4)。
(6)
绘制聚类图,根据需要决定类的个数和类。
3.程序
求解的MATLAB程序如下:
clc, clear
% 名称
ss = {'京津冀', '山西', '内蒙古', '辽宁', '吉林', '黑龙江', '苏沪', '浙江', ...
'安徽', '福建', '江西', '山东', '河南', '湖北', '湖南', '广东', ...
'广西', '海南', '川渝', '云南', '贵州', '西藏', '陕西', '甘肃', ...
'青海', '宁夏', '新疆'};
% 数据
a = [699.70, 1.4371, 0.9364, 0.7804, 10.880; ...
179.46, 1.8982, 1.0006, 0.5870, 11.780; ...
111.13, 1.4180, 0.6772, 0.5158, 17.775; ...
389.60, 1.9182, 0.8541, 0.5762, 26.320; ...
211.34, 1.7880, 1.0798, 0.4569, 19.705; ...
259.00, 2.3059, 0.3417, 0.5076, 23.480; ...
923.19, 3.7350, 2.0572, 0.6208, 22.160; ...
139.29, 1.8712, 0.8858, 0.4536, 12.670; ...
102.78, 1.2333, 0.5326, 0.3798, 27.375; ...
108.50, 1.7291, 0.9325, 0.4687, 11.120; ...
129.20, 3.2454, 1.1935, 0.4519, 17.080; ...
173.35, 1.0018, 0.4296, 0.4503, 21.215; ...
151.54, 1.4927, 0.6775, 0.4738, 13.940; ...
434.46, 7.1328, 2.4413, 0.5282, 19.190; ...
139.29, 2.3501, 0.8360, 0.4890, 14.250; ...
336.54, 3.5407, 1.3863, 0.4020, 22.195; ...
96.12, 1.2288, 0.6382, 0.5000, 14.340; ...
45.43, 2.1915, 0.8648, 0.4136, 8.730; ...
365.01, 1.6801, 1.1486, 0.5720, 18.615; ...
146.00, 6.6333, 2.3785, 0.5359, 12.250; ...
136.22, 2.8279, 1.2918, 0.5984, 10.470; ...
11.79, 4.1514, 1.1798, 0.6118, 7.315; ...
244.04, 5.1194, 1.9682, 0.6287, 17.800; ...
145.49, 4.7515, 1.9366, 0.5806, 11.650; ...
61.36, 8.2695, 0.8598, 0.8098, 7.420; ...
47.60, 1.5078, 0.9587, 0.4843, 9.730; ...
128.67, 3.8535, 1.6216, 0.4901, 14.470];
% 使用zscore函数对矩阵a进行标准化处理
% zscore函数将每列的数据进行标准化,使其均值为0,标准差为1
% 标准化可以将不同变量之间的尺度差异消除,使得它们具有可比性
b = zscore(a)
% 使用pdist函数计算标准化后的矩阵b的成对距离
% pdist函数可以计算多维数据点之间的各种距离,默认情况下,pdist函数计算欧氏距离
d = pdist(b)
% 使用linkage函数进行层次聚类分析
% linkage函数将距离矩阵作为输入,计算聚类之间的链接
% 它返回一个连接矩阵z,该矩阵描述了层次聚类的结构
z = linkage(d)
% 绘制树状图
dendrogram(z, 'label', ss);
4.结果
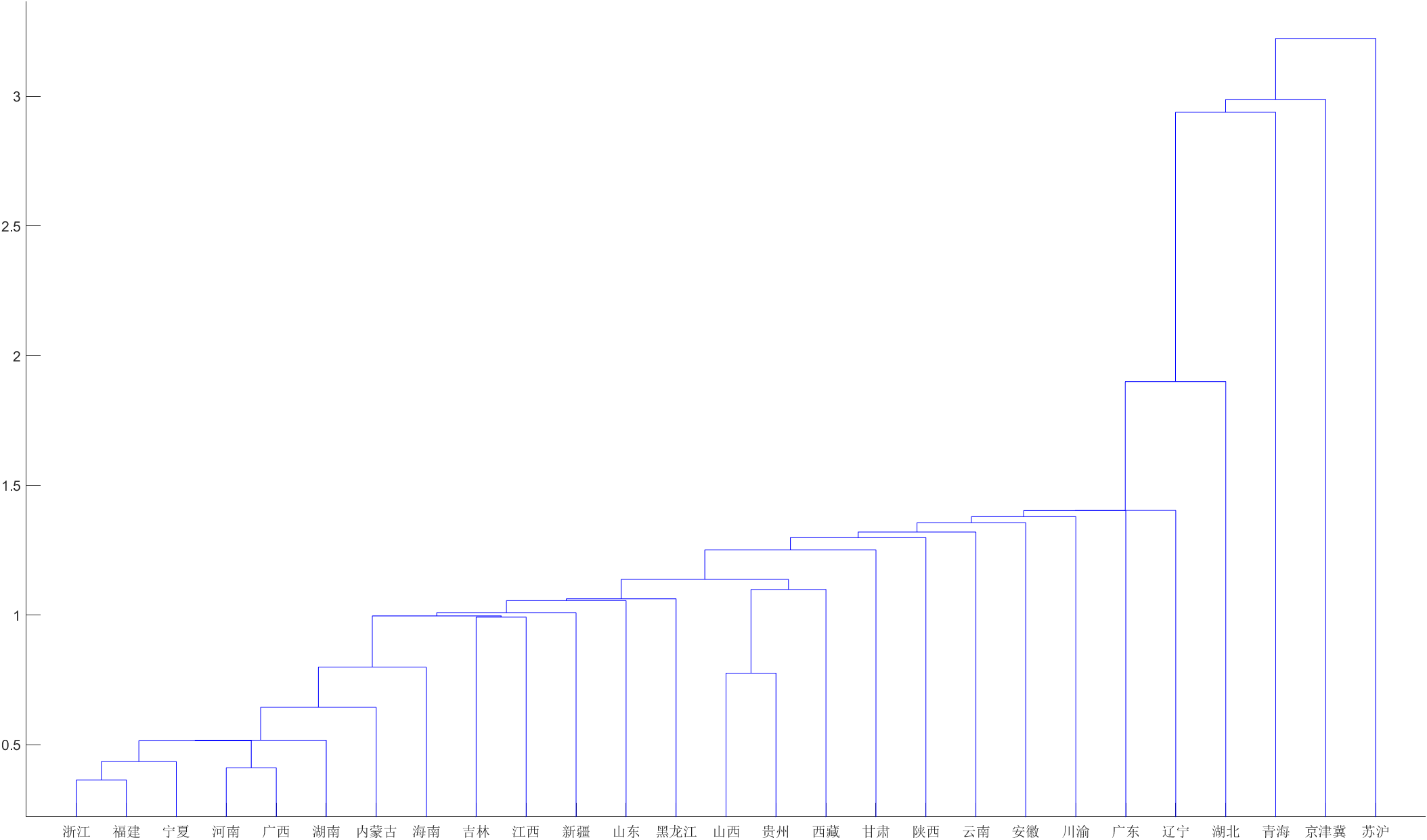
从聚类图可以看出,苏沪、京津冀、青海各自成一类,其余省和自治区成一类。
习题10.2
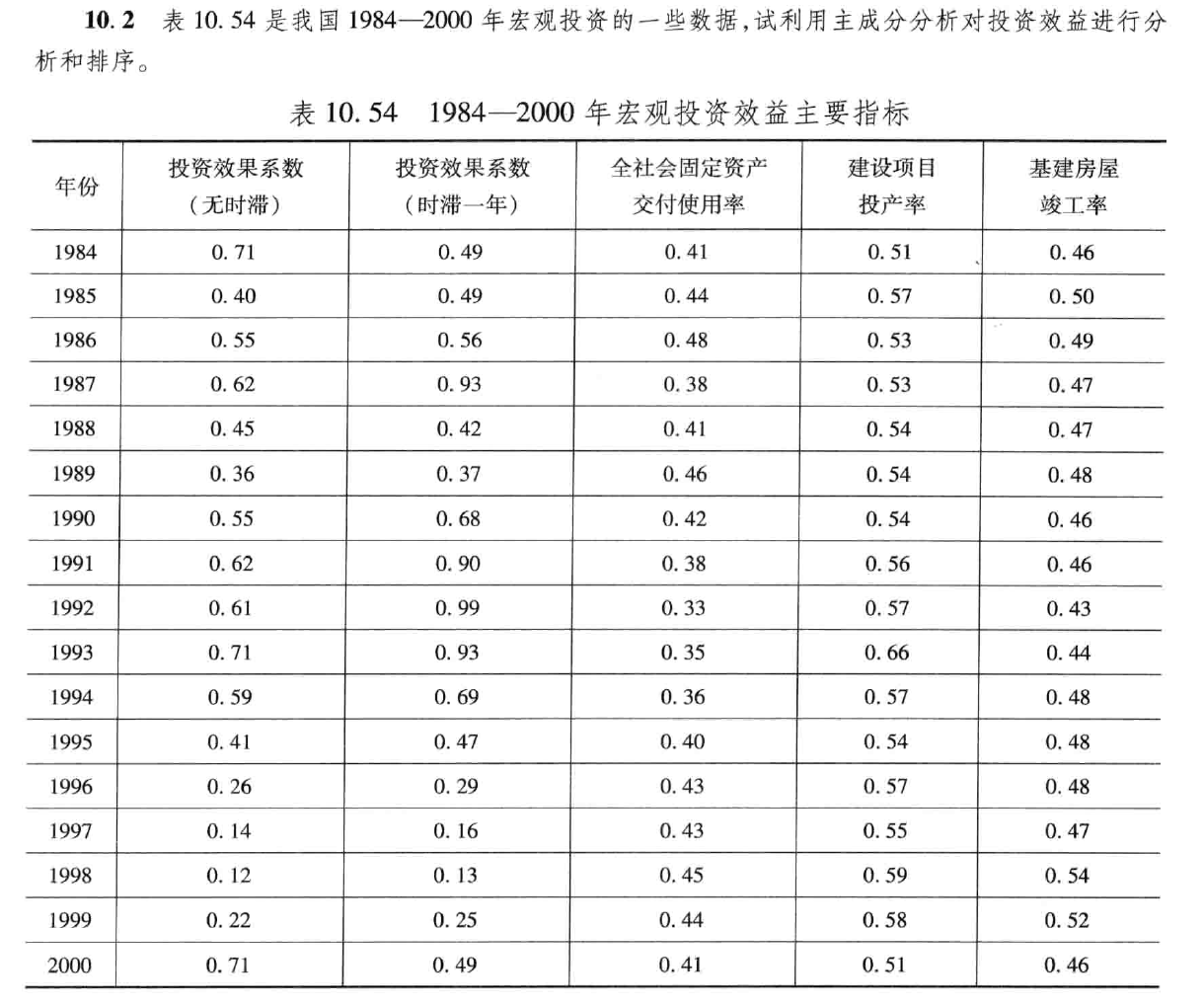
1. 题目要求
2.解题过程
解:
用 \(x_1,x_2,...,x_5\) 分别表示投资效果系数(无时滞),投资效果系数(时滞一年),全社会固定资产交付使用率,建设项目投产率,基建房屋竣工率。
用 \(i=1,2,...,17\) 分别表示1984年,1985年,.. ,2000年,第i年第j个指标变量 \(x_j\) 的取值记作 \(a_ij\) ,构造矩阵 \(A=(a_{ij})_{17*5}\) 。
(1)数据标准化
首先将各指标值 \(a_{ij}\) 转化为标准化指标值: $$ b_{ij}\,=\,{\frac{a_{ij}-\mu_{{i}}}{s_{j}}}\,;i\,=\,1\,,2\,,\cdots,17\,;j\,=\,1\,,\cdots,5. $$ 其中,\(\mu_{j}\) 是第j个指标的样本均值,\(s_j\) 是第j个指标的样本标准差: $$ \tilde{a}{j}\,=\,{\frac{1}{17}}\sum{i=1}^{17}a_{ij} $$
(2)计算相关系数矩阵R $$ R\;=\;(r_{i j})_{\mathrm{5x5}}\, $$
(3)计算特征值和特征向量
计算相关系数矩阵R的特征值,及对应的标准化特征向量 \(u_1,u_2,...,u_5\) ,其中 \(u_{j}=(\,u_{1j},u_{2j},\cdots,u_{3j})^{\mathsf{T}}\) ,由特征向量组成5个新的指标变量: $$ \left{\begin{array}{c} y_{1}=u_{11} \tilde{x}{1}+u{21} \tilde{x}{2}+\cdots+u{51} \tilde{x}{5}, \ y{2}=u_{12} \tilde{x}{1}+u{22} \tilde{x}{2}+\cdots+u{52} \tilde{x}{5}, \ \vdots \ y{5}=u_{15} \tilde{x}{1}+u{25} \tilde{x}{2}+\cdots+u{55} \tilde{x}_{5} . \end{array}\right. $$ 式中,y1是第一主成分,y2是第二主成分,...,y5是第五主成分。
(4)计算综合评价值。
主成分yj的信息贡献率: $$ b_{j}=\frac{\lambda_j}{\sum_{k=1}^{5} \lambda_{k}}\,,j=\,1\,,2\,,\cdots,5 $$ 主成分y1、y2、...、yp的累计贡献率: $$ \alpha_{p}=\frac{\sum_{k=1}^{p} \lambda_{k}}{\sum_{k=1}^{5} \lambda_{k}} $$ 当ap接近于1 (ap = 0.85,0.90,0.95) 时,则选择前p个指标变量作为p个主成分,代替原来5个指标变量,从而可对p个主成分进行综合分析。
计算综合评分: $$ Z\,=\,\sum_{j=1}^{p}\,b_{j}y_{j}. $$ 其中bj是第j个主成分的信息贡献率,根据综合得分值就可以进行评价。
利用Matlab求得相关系数矩阵的前5个特征根及其贡献率如下表:
| 序号 | 特征根 | 贡献率 | 累计贡献率 |
|---|---|---|---|
| 1 | 3.1343 | 62.6866 | 62.6866 |
| 2 | 1.1683 | 23.3670 | 86.0536 |
| 3 | 0.3502 | 7.0036 | 93.0572 |
| 4 | 0.2258 | 4.5162 | 97.5734 |
| 5 | 0.1213 | 2.4266 | 100.0000 |
可以看出,前三个特征根的累计贡献率就达到93%以上,主成分分析效果很好。下面选取前三个主成分进行综合评价。前三个特征根对应的特征向量如下表:
| x1 | x2 | x3 | x4 | x5 | |
|---|---|---|---|---|---|
| 第1特征向量 | 0.490542 | 0.525351 | -0.48706 | 0.067054 | -0.49158 |
| 第2特征向量 | -0.29344 | 0.048988 | -0.2812 | 0.898117 | 0.160648 |
| 第3特征向量 | 0.510897 | 0.43366 | 0.371351 | 0.147658 | 0.625475 |
由此可得三个主成分分别为: $$ \begin{array}{l}{{y_{1}~=0.491\tilde{x}{1}+0.525\tilde{x}{2}-0.487\tilde{x}{3}+0.067\tilde{x}{5}-0.492\tilde{x}{5}\,,}}\ {{y{2}~=-0.293\tilde{x}{1}+0.049\tilde{x}{2}-0.898\tilde{x}{4}+0.161\tilde{x}{5}\,,}}\ {{y_{3}~=0.511\tilde{x}{1}+0.434\tilde{x}{1}+0.43\tilde{x}{2}+0.148\tilde{x}{4}+0.625\tilde{x}_{5}\,,}}\end{array} $$ 分别以三个主成分的贡献率为权重,构建主成分综合评价模型为: $$ Z = 0.6269y_1 + 0.2337y_2 + 0.076y_3 $$ 把各年度的三个主成分值代入上式,可以得到各年度的综合评价值以及排序结果如下表:
| 年代 | 1993 | 1992 | 1991 | 1994 | 1987 | 1990 | 1984 | 2000 | 1995 |
|---|---|---|---|---|---|---|---|---|---|
| 名次 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 综合评价值 | 2.4464 | l.9768 | 1.1123 | 0.8604 | 0.8456 | 0.2258 | 0.0531 | 0.0531 | -0.2534 |
| 年代 | 1988 | 1985 | 1996 | 1986 | 1989 | 1997 | 1999 | 1998 |
|---|---|---|---|---|---|---|---|---|
| 名次 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 综合评价值 | 0.2662 | 0.5292 | 0.7405 | 0.7789 | 0.9715 | 1.1476 | -1.2015 | -1.6848 |
3.程序
求解的MATLAB程序如下:
clc, clear
gj = [0.71, 0.49, 0.41, 0.51, 0.46; ...
0.40, 0.49, 0.44, 0.57, 0.50; ...
0.55, 0.56, 0.48, 0.53, 0.49; ...
0.62, 0.93, 0.38, 0.53, 0.47; ...
0.45, 0.42, 0.41, 0.54, 0.47; ...
0.36, 0.37, 0.46, 0.54, 0.48; ...
0.55, 0.68, 0.42, 0.54, 0.46; ...
0.62, 0.90, 0.38, 0.56, 0.46; ...
0.61, 0.99, 0.33, 0.57, 0.43; ...
0.71, 0.93, 0.35, 0.66, 0.44; ...
0.59, 0.69, 0.36, 0.57, 0.48; ...
0.41, 0.47, 0.40, 0.54, 0.48; ...
0.26, 0.29, 0.43, 0.57, 0.48; ...
0.14, 0.16, 0.43, 0.55, 0.47; ...
0.12, 0.13, 0.45, 0.59, 0.54; ...
0.22, 0.25, 0.44, 0.58, 0.52; ...
0.71, 0.49, 0.41, 0.51, 0.46];
gj = zscore(gj); % 将矩阵 gj 进行标准化处理,使得每一列的数据具有零均值和单位方差
r = corrcoef(gj); % 计算矩阵 gj 的相关系数矩阵 r,用于后续的主成分分析
% 使用函数 pcacov 对相关系数矩阵 r 进行主成分分析
% 它返回三个输出变量 x、y 和 z,分别表示主成分的系数矩阵、特征值和贡献率
[x, y, z] = pcacov(r)
% 生成一个与 x 大小相同的矩阵 f,其中每个元素的值为主成分系数的符号
% 这样做是为了确保主成分方向一致
f = repmat(sign(sum(x)), size(x, 1), 1);
x = x .* f % 将主成分系数矩阵 x 的每个元素与 f 对应位置的元素相乘,以确保主成分方向一致
num = 3; % 保留的主成分数量
df = gj * x(:, 1:num); % 计算投资数据矩阵 gj 与前 num 个主成分系数的乘积,得到降维后的数据矩阵 df
tf = df * z(1:num) / 100; % 计算降维后数据矩阵 df 与前 num 个特征值的乘积,并进行缩放,得到投资效益值的估计
[stf, ind] = sort(tf, 'descend'); % 对投资效益值进行降序排序,并返回排序后的结果 stf 和对应的索引 ind
stf = stf', ind = ind'
4.结果

各年度的综合评价值以及排序结果如下表:
| 年代 | 1993 | 1992 | 1991 | 1994 | 1987 | 1990 | 1984 | 2000 | 1995 |
|---|---|---|---|---|---|---|---|---|---|
| 名次 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 综合评价值 | 2.4464 | l.9768 | 1.1123 | 0.8604 | 0.8456 | 0.2258 | 0.0531 | 0.0531 | -0.2534 |
| 年代 | 1988 | 1985 | 1996 | 1986 | 1989 | 1997 | 1999 | 1998 |
|---|---|---|---|---|---|---|---|---|
| 名次 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 综合评价值 | 0.2662 | 0.5292 | 0.7405 | 0.7789 | 0.9715 | 1.1476 | -1.2015 | -1.6848 |